問題
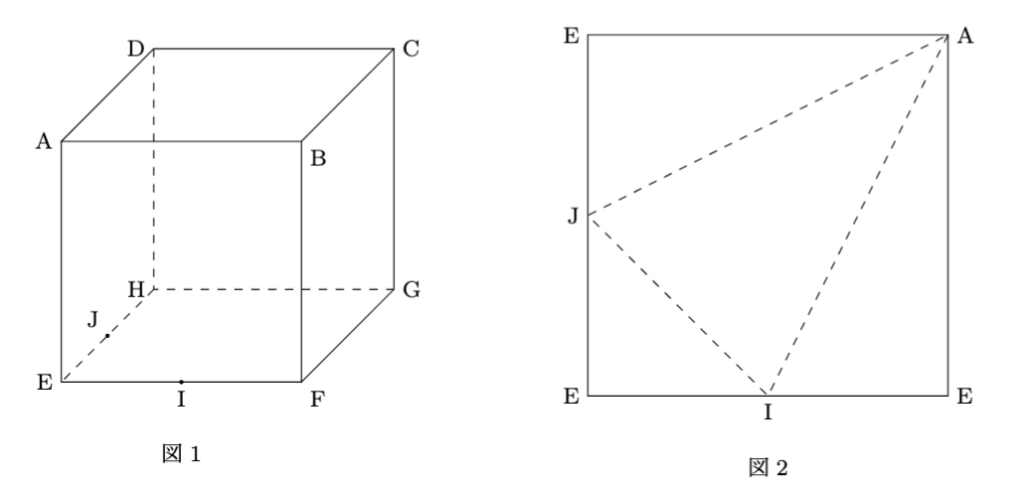
図1は1辺の長さが6cmの立方体である. 点Iと点Jはそれぞれ辺EFと辺EHの真ん中の点である. 但し, この立方体を点A, I, Jを通る平面で切断したときにできる三角錐AEIJの展開図の一つは, 図2のように正方形になることがわかっている. 次の問に答えよ.
解説
- (1) 三角錐AEIJの体積を求めよ.
- 三角錐の体積は$\fbox{底面積}\times\fbox{高さ}\div3$で求められるので, $3\times3\times6\div3=18$より, 18cm$^{3}$となります.
- (2) この立方体を点D, I, Jを通る平面で切断した. 切断面の面積を求めよ.
- 点D, I, Jを通る平面で切断すると, 切断面は$\mathrm{JD}=\mathrm{IB}$の等脚台形となります. ここで, 図2をヒントに, 等脚台形を正方形に埋め込むと,
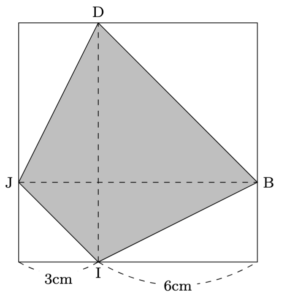
から, $9\times9\div2=40.5$より, 面積は40.5cm$^{2}$となります.
- 点D, I, Jを通る平面で切断すると, 切断面は$\mathrm{JD}=\mathrm{IB}$の等脚台形となります. ここで, 図2をヒントに, 等脚台形を正方形に埋め込むと,
- (3) この立方体を点D, I, Jを通る平面と, 点A, I, Cを通る平面で切断した. このとき, 点Gを含む方の立体の表面積を求めよ.
- 2箇所の切断面を立方体に反映させると,
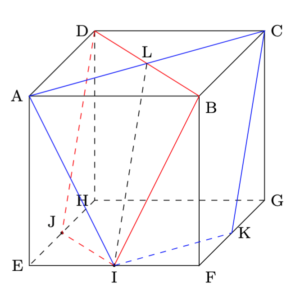
から, Gを含む立体の表面積は,
$\fbox{三角形LCD}+\fbox{三角形CKG}+\fbox{三角形DJH}$
$+\fbox{正方形DHGC}+\fbox{平行四辺形LIKC}+\fbox{平行四辺形DJIL}+\fbox{五角形IKGHJ}$
$\\$
$=6\times6\div4+3\times6\div2+3\times6\div2$
$+6\times6+40.5\times\dfrac{2}{3}+40.5\times\dfrac{2}{3}+(6\times6-3\times3\div2\times2)$
$\\$
$=9+9+9+36+27+27+27$
$\\$
$=144$より, 表面積は144cm$^{2}$となります.
- 2箇所の切断面を立方体に反映させると,


