問題
図は1辺4cmの正方形と, 半径2cmで中心角90$^{\circ}$の扇形を4つ組み合わせた図形で, 辺AD上に$\mbox{AM}=1\mbox{cm}$となるような点MWOをとります. また, 辺BC上のFとCの間に点Pをとり, 2点M, Pを結び, 図のように影のついた部分をそれぞれア, イ, ウとします. 次の問に答えなさい.
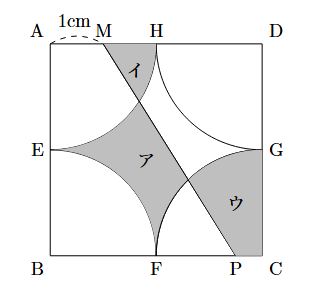
① $\mbox{CP}=1\mbox{cm}$のとき, ア, イ, ウの面積の和を求めなさい.
$\mathrm{AM}=\mathrm{CP}$より, 以下のように記号を振ると,
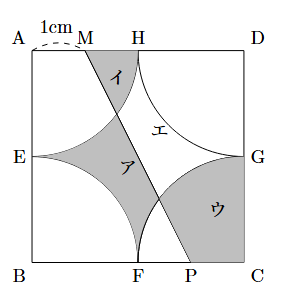
アの面積とエの面積も等しくなるので,
$\text{ア}+\text{イ}+\text{ウ}=\text{エ}+\text{イ}+\text{ウ}$
$\text{エ}+\text{イ}+\text{ウ}+\text{扇形DGH}=\text{台形CPMD}$
$\text{エ}+\text{イ}+\text{ウ}=\text{台形CPMD}-\text{扇形DGH}$
$=(1+3)\times4\times\dfrac{1}{2}-2\times2\times3.14\times\dfrac{1}{4}$
$=$$4.86\mathrm{cm}^2$
となります.
② アの面積と, イとウを合わせた面積が等しいとき, CPの長さを求めなさい.
以下のように記号を振ると,
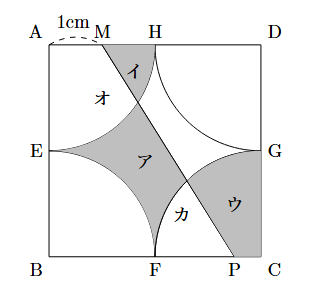
$\text{ア}=\text{イ}+\text{ウ}$
$\text{ア}+\text{オ}+\text{カ}=\text{イ}+\text{オ}+\text{ウ}+\text{カ}$
$\text{台形AMPB}-\text{扇形BEF}=\text{扇形AHM}+\text{扇形CGF}$
$\text{台形AMPB}=\text{扇形AHM}+\text{扇形CGF}+\text{扇形BEF}$
$=2\times2\times3.14\times\dfrac{1}{4}\times3$
$=9.42\mathrm{cm}^2$
より,
$9.42=(1+\mathrm{BP})\times4\times\dfrac{1}{2}$
$\mathrm{BP}=3.71\mathrm{cm}$
から, CPの長さは0.29cmとわかります.

