問題
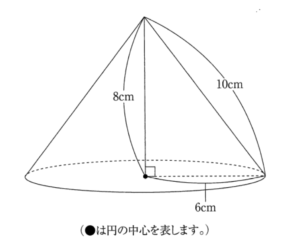
- 下のような円錐があります。これについて, 次の問に答えなさい。
- $(1)$ この円錐の体積は何cm$^{3}$ですか。
$\\$ - $(2)$ この円錐を展開図に表すと, 側面は扇形になります。その扇形の中心角の大きさは何度ですか。
$\\$ - $(3)$ この円錐の表面積は何cm$^{2}$ですか。
- $(1)$ この円錐の体積は何cm$^{3}$ですか。
解答解説
- 下のような円錐があります。これについて, 次の問に答えなさい。
- $(1)$ この円錐の体積は何cm$^{3}$ですか。
円錐の体積は, $\fbox{半径}\times\fbox{半径}\times3.14\times\fbox{高さ}\times\frac{1}{3}$で求められるので,
$6\times6\times3.14\times8\times\frac{1}{3}=301.44$より, $\underline{301.44\mbox{cm}^{3}}$となります.
$\\$ - $(2)$ この円錐を展開図に表すと, 側面は扇形になります。その扇形の中心角の大きさは何度ですか。
問われている扇形の中心角については, $\frac{\fbox{半径}}{\fbox{母線}}=\frac{\fbox{中心角}}{360\mbox{度}}$という関係が成り立つので,
$\frac{6}{10}=\frac{\fbox{中心角}}{360\mbox{度}}$より, $\underline{216\mbox{度}}$となります.
$\\$ - $(3)$ この円錐の表面積は何cm$^{2}$ですか。
(2)をヒントに展開図を考えると, 半径10cmで中心角216度の扇形と半径6cmの円に分割できるので,
$10\times10\times3.14\times\frac{216}{360}+6\times6\times3.14=301.44$より, 表面積は$\underline{301.44\mbox{cm}^{2}}$になります.
- $(1)$ この円錐の体積は何cm$^{3}$ですか。