- 問題
- 解説
- (1) 設定が$\dfrac{1}{2}$, 長さが600mの時間床がA地点からB地点の間に敷かれています. このとき, 太郎君がB地点に到着したのは12時何分何秒ですか.
- (2) 設定が$\dfrac{1}{2}$の時間床がA地点からB地点の間の一部に敷かれていて, 太郎君がB地点に到着したのは12時3分20秒でした. このとき, 時間床の長さを求めなさい.
- (3) 設定が$\dfrac{1}{2}$, 長さが500mの時間床がA地点からB地点の間に敷かれています. 太郎君が時間床に乗ってから440m移動したところで設定を変えたら, B地点に到着したのは12時3分6秒でした. 時間床の設定は$\dfrac{1}{2}$からいくつに変えましたか.
- (4) A地点とB地点の間で, A地点から400m離れた地点をC地点とします. 設定が$\dfrac{1}{3}$の時間床がC地点からある場所まで敷かれています. 12時1分57秒に設定を$\dfrac{5}{3}$に変えたら, 太郎君がB地点に到着したのは12時4分28秒でした. このとき, 時間床の長さを求めなさい.
問題
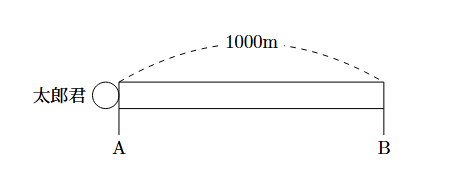
太郎君は, 人が床の上に乗っているときに, その人が床に乗っていて感じた時間と, 実際に経過した時間が異なる床, 「時間床」を開発しました. 時間床には変えることのできる「設定」があります. 長さが200mの時間床の上を秒速4mで移動すると, 乗っていて感じた時間は50秒間でしたが, 設定が$\dfrac{1}{2}$のときは実際の時間を表す時計ではその$\dfrac{1}{2}$倍である25秒が経過して, 設定が$\dfrac{3}{2}$のときは実際の時間を表す時計ではその$\dfrac{3}{2}$倍である75秒が経過していました. 太郎君が12時ちょうどに秒速4mでA地点を出発し, 1000m離れたB地点移動するとき, 次の問に答えなさい. 但し, ここでの時刻は, 実際の時間を表す時計の時刻とします.
解説
(1) 設定が$\dfrac{1}{2}$, 長さが600mの時間床がA地点からB地点の間に敷かれています. このとき, 太郎君がB地点に到着したのは12時何分何秒ですか.
時間床でない部分は$1000-600=400\mbox{m}$で, $400\div4=100$秒かかります.
また, 時間床の上では, 太郎君が感じる時間は$600\div4=150$秒ですが, 設定が$\dfrac12$なので, 実際の時間は$150\times\dfrac12=75$秒となります.
以上から, 全体でかかる時間は, $100+75=175$秒なので, 到着時刻は, $12\text{時}2\text{分}55\text{秒}$となります.
(2) 設定が$\dfrac{1}{2}$の時間床がA地点からB地点の間の一部に敷かれていて, 太郎君がB地点に到着したのは12時3分20秒でした. このとき, 時間床の長さを求めなさい.
移動時間を考えると, 3分20秒($3\times60+20=200$秒)より, 時間床の長さを$\square\mbox{m}$とすると, 時間床でない部分は $1000-\square\mbox{m}$となります.
普通の床でかかる時間は, $\dfrac{1000-\square}{4}$秒, 時間床の部分でかかる時間は, 感じる時間が$\square\div4$秒で, 設定が$\dfrac12$なので
$\dfrac12\times\dfrac{\square}{4}=\dfrac{\square}{8}$秒です.
これらを合わせると200秒になるので,
\[
\dfrac{1000-\square}{4}+\dfrac{\square}{8}=200
\]
両辺を8倍すると,
\[
2\times(1000-\square)+\square=1600
\]
\[
2000-\square=1600
\]
\[
\square=400
\]
よって, 時間床の長さは $400\mbox{m}$ となります.
(3) 設定が$\dfrac{1}{2}$, 長さが500mの時間床がA地点からB地点の間に敷かれています. 太郎君が時間床に乗ってから440m移動したところで設定を変えたら, B地点に到着したのは12時3分6秒でした. 時間床の設定は$\dfrac{1}{2}$からいくつに変えましたか.
移動時間を考えると3分6秒($3\times60+6=186$秒)より, 時間床でない部分は $1000-500=500\mbox{m}$ なので, その部分にかかる実際の時間は$500\div4=125$秒となります.
また, 時間床に乗ってから設定を変えるまでに移動した距離は440mなので, この部分に感じる時間は$440\div4=110$秒, 設定は$\dfrac12$なので, 実際の時間は$110\times\dfrac12=55$秒となります.
残りの時間床の長さは $500-440=60\mbox{m}$ で, この部分に感じる時間は $60\div4=15$秒だから, 設定を$\triangle$とすると, 実際の時間は $15\times\triangle$秒となります.
ここでかかった時間の合計は186秒とわかっているので,
\[
125+55+15\times\triangle=186
\]
\[
180+15\times\triangle=186
\]
\[
15\times\triangle=6
\]
\[
\triangle=\dfrac{2}{5}
\]
よって, 設定は $\dfrac12$から $\dfrac25$ に変えたことが分かります.
(4) A地点とB地点の間で, A地点から400m離れた地点をC地点とします. 設定が$\dfrac{1}{3}$の時間床がC地点からある場所まで敷かれています. 12時1分57秒に設定を$\dfrac{5}{3}$に変えたら, 太郎君がB地点に到着したのは12時4分28秒でした. このとき, 時間床の長さを求めなさい.
まず, AからCまでは普通の床で, 長さは400mなので, 実際の時間は$400\div4=100$秒かかり, Cに着く時刻は12時1分40秒です.
12時1分57秒は, 12時1分40秒から17秒後なので, 設定が$\dfrac13$の時間床の上を17秒間進んだことになります.
設定が$\dfrac13$のとき, 実際の時間17秒に対応する感じる時間は, $17\div\dfrac13=51$秒なので, その間に進んだ距離は$51\times4=204\mbox{m}$ です.
よって, C地点から204m進んだ地点で設定を変えたことになります.
ここで, 時間床の長さを$\square\mbox{m}$とすると, 設定変更後の時間床の残りの長さは
$\square-204\mbox{m}$, その先Bまでの普通の床の長さは
$1000-(400+\square)=600-\square\mbox{m}$ です.
次に, Bに着くまでの実際の時間を考えると, 設定を変えてからBに着くまでの全体の実際の時間は, 12時4分28秒と12時1分57秒の差なので,
\[
(4\text{分}28\text{秒})-(1\text{分}57\text{秒})
=2\text{分}31\text{秒}=151\text{秒}
\]
です.
設定を$\dfrac53$にした時間床の部分について, 感じる時間は
$(\square-204)\div4$秒なので, 実際の時間は$\dfrac53\times\dfrac{\square-204}{4}=\dfrac{5\times(\square-204)}{12}\ \text{秒}$で, 残りの普通の床 $(600-\square)\mbox{m}$ にかかる実際の時間は$(600-\square)\div4$秒となります.
これらの和が151秒なので,
\[
\dfrac{5\times(\square-204)}{12}+\dfrac{600-\square}{4}=151
\]
両辺を12倍して整理すると,
\[
5\times(\square-204)+3\times(600-\square)=1812
\]
\[
5\times\square-1020+1800-3\times\square=1812
\]
\[
2\times\square+780=1812
\]
\[
\square=516
\]
よって, 時間床の長さは $516\mbox{m}$ です.

