問題
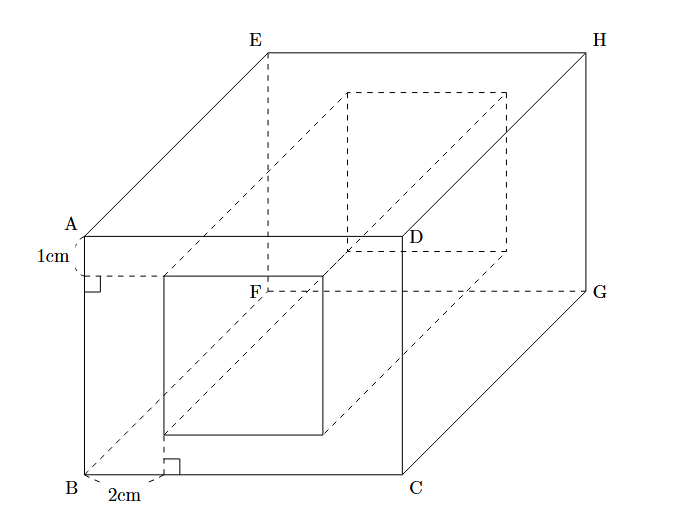
図のように, $\mbox{AB}=6\mbox{cm}$, $\mbox{AD}=8\mbox{cm}$, $\mbox{AE}=12\mbox{cm}$の直方体ABCD-EFGHから, 1辺の長さが4cmである正方形を底面とする直方体で真っ直ぐ奥まで刳り貫いた立体があります. 次の問に答えなさい.
解説
(1) この立体の体積と表面積をそれぞれ求めなさい.
元の直方体の体積は, $6\times8\times12=576\mbox{cm}^3$で, 刳り貫いた直方体は, 底面が $4\mbox{cm}\times4\mbox{cm}$, 高さが$12\mbox{cm}$なので,
体積は$4\times4\times12=192\mbox{cm}^3$より, 立体の体積は, $576-192=$$384\mbox{cm}^3$ となります.
次に表面積を考えると, 元の直方体の表面積は, $2\times(6\times8+8\times12+6\times12)=2\times(48+96+72)=2\times216=432\mbox{cm}^2$で,
刳り貫くことにより, 前面と背面から $4\mbox{cm}\times4\mbox{cm}$の部分が2枚分取り除かれ, 一方で, 穴の周囲に $4\mbox{cm}\times12\mbox{cm}$の面が4枚生じるので, 最終的な表面積の増減は, $432-4\times4\times2+4\times4\times12=432-32+192=$$592\mbox{cm}^2$となります.
(2) 辺AD, BC, EHの真ん中の点をそれぞれP, Q, Rとします. この立体を3点P, Q, Rを通る平面で切断したとき, 点Aを含む方の立体をKとします. 立体Kの表面積を求めなさい.
3点P, Q, Rはいずれも元の直方体の左右の真ん中にあるので, この切断面は, 直方体の左右を2つに分ける平面となり, 立体Kと, 反対側の立体は形も大きさも等しく, 2つ合わせると元の立体になるとわかります.(切断したことで, 新しく切り口の面が2枚できることに注意)
以上を踏まえて, 切り口の断面積を求めると, 立体全体の断面(PQRを通る平面での断面)は, 縦$6\mbox{cm}$, 奥行き$12\mbox{cm}$の長方形なので, 面積は$6\times12=72\mbox{cm}^2$となります.
この中で, 穴の部分にあたるのは, 縦$4\mbox{cm}$, 奥行き$12\mbox{cm}$の長方形で, 面積は$4\times12=48\mbox{cm}^2$なので, 立体の断面積は, $72-48=24\mbox{cm}^2$ となります.
ここで, 立体Kと反対側の立体を合わせ表面積を考えると, $592+2\times24=640\mbox{cm}^2$より, 立体Kの表面積はその半分となるので, $640\div2=$$320\mbox{cm}^2$となります.
(3) (2)の立体Kにおいて, 辺AE, PRの真ん中の点をそれぞれS, Tとし, 辺BF上に$\mbox{BU}=4\mbox{cm}$となる点Uをとります. 立体Kを3点S, T, Uを通る平面で切断したとき, 点Aを含む方の立体の体積を求めなさい.
Aを含む立体について, 内側を刳り貫く前の直方体として, 平均の高さを考えると,
$(6+4)\times2\div4=5\mbox{cm}$より,
求める体積は$6\times4\times5-4\times2\times5=$$80\mbox{cm}^3$となります.

