[中学受験算数]角度を求めてみよう！〜頻出パターン4選〜〜

平行線を利用する

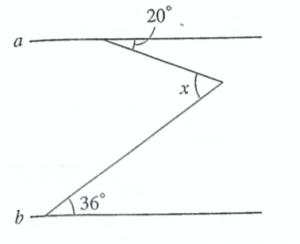＊但し、$a$と$b$は平行

この手のパターンは$x$のところに$a,b$に平行な補助線を引くと、すぐに解けます。

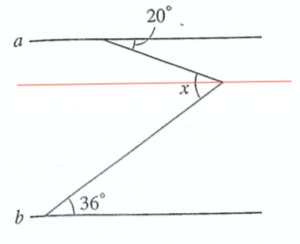
錯角の性質を利用し、

$\mathrm{\angle }x={20}^{\circ }+{36}^{\circ }$
$={56}^{\circ }$

正多角形の公式を利用する

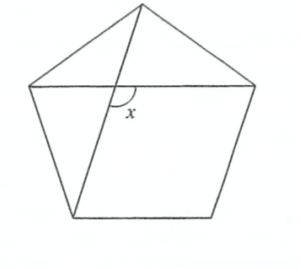＊但し、図形は正五角形

正N角形の1つの内角の大きさを求める公式は、

${180}^{\circ }\times (N-2)÷N$

なので、今回は正五角形、N=5で計算すると、1つの内角の大きさは、

${180}^{\circ }\times 3÷5={108}^{\circ }$

より、108°とわかります。

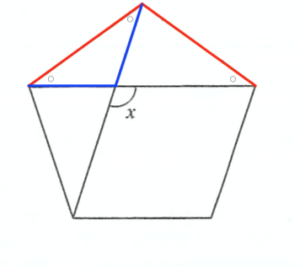
また、赤線部と青線部の長さはそれぞれ等しいので、⚪︎印の角度は全て等しくなります。

${108}^{\circ }+\text{⚪︎}\times 2={180}^{\circ }$

より、$\mathrm{\angle }x={108}^{\circ }$とわかります。

折り返しを利用する

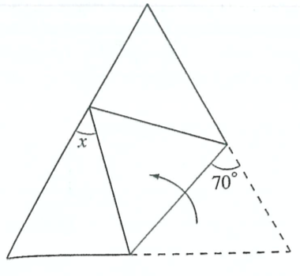＊但し、図形は正三角形

正三角形の1つの内角の大きさは60°、折り返した箇所に対応する角度は互いに等しくなるので、

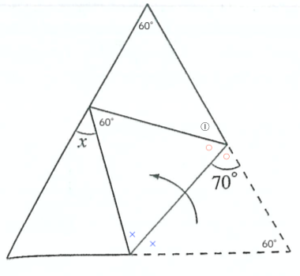
$\text{①}={180}^{\circ }-{70}^{\circ }\times 2$
$={40}^{\circ }$
${60}^{\circ }+\text{①}={60}^{\circ }+\mathrm{\angle }x$
$\mathrm{\angle }x={40}^{\circ }$

より、$\mathrm{\angle }x={40}^{\circ }$とわかります。

等しい角度を置き換える

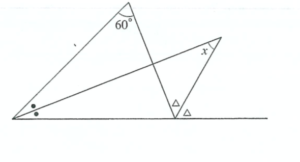＊但し、同じ印は同じ角度を表す

角度についての情報を整理して、式に表すと、

$\text{●}\times 2+{60}^{\circ }=\text{△}\times 2$
$\text{△}=\text{●}+{30}^{\circ }$

$\text{●}+\mathrm{\angle }x=\text{△}$

から、△についてまとめると、

$\text{△}=\text{●}+{30}^{\circ }$
$=\text{●}+\mathrm{\angle }x$

より、$\mathrm{\angle }x={30}^{\circ }$とわかります。