問題
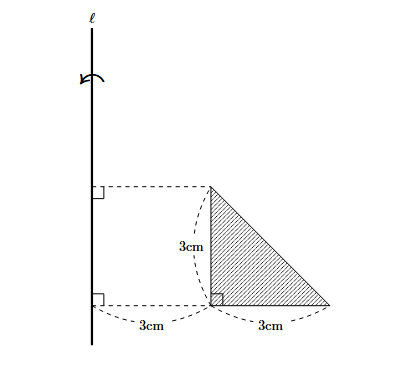
下の図において, 斜線部分の三角形を直線ℓの周りに1回転してできる立体の体積は$\fbox{ }$cm$^{3}$である.
解説
回転した立体を考えると, 円錐台(大きな円錐(底面が半径6cmの円で高さが6cm)から小さな円錐(底面が半径3cmの円で高さが3cm)を引いた立体)から円柱(底面が半径6cmの円で高さが3cm)を切り取った形だとわかります.
ここで, 大きな円錐と小さな円錐の体積比は, 相似比$1:2$より$1:8$なので, 円錐台の体積は, 大きな円錐の$\dfrac{7}{8}$倍であるとわかります.
以上より, 求める体積は,
$6\times6\times3.14\times6\times\dfrac{1}{3}\times\dfrac{7}{8}-3\times3\times3.14\times3$
$=(63-27)\times3.14=113.04$から, $\fbox{ }=$$113.04(\mathrm{cm}^{3})$とわかります.


