問題
1から100までの整数の中に、6でも8でも割り切れない数は何個ありますか。
解説
問題文にある、「6でも8でも割り切れない数」を直接求めるのは難しいので、先に「6か8で割り切れる数」を求めた後に、全体から引くという考え方をします。
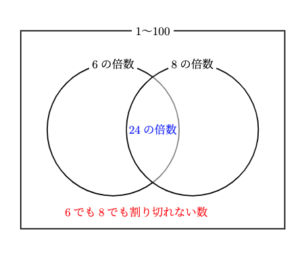
ここで、以下のようにヴェン図を書いて、整数を整理すると、
- 6で割り切れる数=6の倍数
- 8で割り切れる数=8の倍数
- 6でも8でも割り切れる数=24(6と8の最小公倍数)の倍数
- 6でも8でも割り切れない数
となります。
次にそれぞれの集合の個数を求めると、
- 6の倍数
\(100\div6=16\cdots4\)
より16個 - 8の倍数
\(100\div8=12\cdots4\)
より12個 - 24の倍数
\(100\div24=4\cdots4\)
より4個
となるので、6か8で割り切れる数の個数は、
\(16+12-4=24\)
より、24個とわかります。(この時、4を引き忘れないように注意)
最後に、6でも8でも割り切れない数の個数を求めると、
\(100-24=76\)
より76個とわかります。(うっかり、24個で計算を終えないように注意!)