問題
下の図で, 三角形ABCは, 辺BCが3cm, 辺ACが7cm, 角Cの大きさが54$^{\circ}$である. また, 三角形DECは, 三角形ABCを点Cを中心に, 辺BCと辺CDが一直線になるように回転させたものである. このとき, 斜線部分の面積は◻︎cm$^{2}$である.
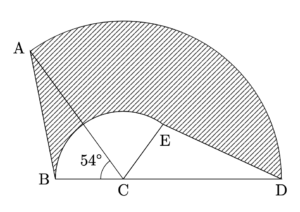
解説
以下のように補助線を引くと,
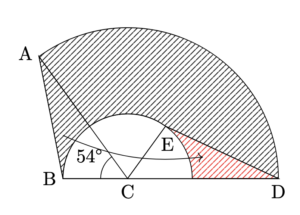
矢印のように移動できるので, 斜線部分の面積は,
$7\times7\times3.14\times\dfrac{126^{\circ}}{360^{\circ}}-3\times3\times3.14\times\dfrac{126^{\circ}}{360^{\circ}}$
$\\$
$=(49-9)\times3.14\times\dfrac{126^{\circ}}{360^{\circ}}$
$\\$
$=14\times3.14=43.96$
より, 43.96cm$^{2}$となります.


