問題
- ある文房具店では, 52円切手と82円切手と92円切手の3種類の切手を売っています。このとき, 次のそれぞれの場合について答えなさい。
- $(1)$ Aさんは, 82円切手を1枚も買わないで, 52円切手と92円切手を合わせて20枚買ったところ, 代金の合計は1200円になりました。Aさんが買った92円切手は何枚ですか。
- $(2)$ Bさんは, 52円切手と82円切手と92円切手を合わせて30枚買ったところ, 代金の合計は2160円になりました。このときに買った52円切手の枚数と82円切手の枚数は同じでした。3種類の切手をそれぞれ何枚買いましたか。
- $(3)$ Cさんは, 52円切手と82円切手と92円切手を合わせて40枚買ったところ, 代金の合計は2750円になりました。このとき, Cさんが買った3種類の切手の枚数の組として考えられるものを全て求め, それぞれの枚数の組みを書きなさい。但し, どの種類の切手も, 1枚以上は買ったものとします。
解答解説
- ある文房具店では, 52円切手と82円切手と92円切手の3種類の切手を売っています。このとき, 次のそれぞれの場合について答えなさい。
- $(1)$ Aさんは, 82円切手を1枚も買わないで, 52円切手と92円切手を合わせて20枚買ったところ, 代金の合計は1200円になりました。Aさんが買った92円切手は何枚ですか。
以下のような面積図を用いると, $\fbox{92円切手の枚数}\times(92-52)=1200-52\times20$より, 92円切手の枚数は$\underline{4\mbox{枚}}$となります.

- $(2)$ Bさんは, 52円切手と82円切手と92円切手を合わせて30枚買ったところ, 代金の合計は2160円になりました。このときに買った52円切手の枚数と82円切手の枚数は同じでした。3種類の切手をそれぞれ何枚買いましたか。
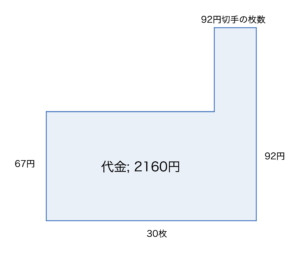
52円切手と82円切手を同じ枚数買ったということは, $(52+82)\div2=67$円切手を2倍買ったことと同義なので, (1)同様面積図を用いると, $\fbox{92円切手の枚数}\times(92-67)=2160-67\times30$より, 92円切手の枚数は6枚, 67円切手の枚数は24枚とそれぞれわかります. ここで67円切手は, 52円切手と82円切手を同じ枚数買ったときの平均であるので, それぞれの枚数は12枚ずつとわかります.
以上より購入した切手の枚数は, $\underline{52\mbox{円切手が}12\mbox{枚}, 82\mbox{円切手が}12\mbox{枚}, 92\mbox{円切手が}6\mbox{枚}}$となります.
- $(3)$ Cさんは, 52円切手と82円切手と92円切手を合わせて40枚買ったところ, 代金の合計は2750円になりました。このとき, Cさんが買った3種類の切手の枚数の組として考えられるものを全て求め, それぞれの枚数の組みを書きなさい。但し, どの種類の切手も, 1枚以上は買ったものとします。
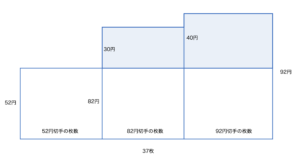
各切手を1枚は買っているので, $40-3=37$枚で合計代金$2750-(52+82+92)=2524$円になったと考えます. ここで, (1), (2)同様, 面積図を用いると, 着色部分の面積について以下の式が成り立ちます.
$30\times\fbox{82円切手の枚数}+40\times\fbox{92円切手の枚数}=2524-52\times37=600$\\
また, この式の両辺を10で割ると,
$3\times\fbox{82円切手の枚数}+4\times\fbox{92円切手の枚数}=60$\\
となり, これを満たす数を調べると, (82円切手の枚数, 92円切手の枚数)=(0, 15), (4, 12), (8, 9), (12, 6), (16, 3), (20, 0)の6通り見つかります.
以上より, 各切手の枚数は, $\underline{(52\mbox{円切手の枚数}, 82\mbox{円切手の枚数}, 92\mbox{円切手の枚数})=(23, 1, 16), (22, 5, 13), (21, 9, 10), (20, 13, 7), (19, 17, 4), (18, 21, 1)}$となります.
- $(1)$ Aさんは, 82円切手を1枚も買わないで, 52円切手と92円切手を合わせて20枚買ったところ, 代金の合計は1200円になりました。Aさんが買った92円切手は何枚ですか。


