問題
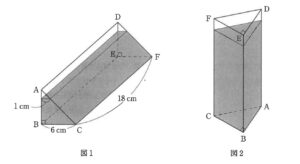
底面が直角二等辺三角形の三角柱の容器に水が入っています。この容器を水平な机の上に置きます。はじめは、図1のように面BDFEを下にして置きます。その後、図2のように面ABCを下にして置きます。
- (1) 図2の水面の高さは何cmですか。
- (2) 図2の状態から、容器の外にある量の水を出したところ、水面の高さが7.5cm低くなりました。その後、図1のように面BCFEを下にして置いたとき、水面の高さは何cmになりますか。
解説
- (1) まずは、図1から水の容積を求めると、
\((6\times6\div2-1\times1\div)\times18\)
\(=17.5\times18\)
より、\(17.5\times18\)㎠とわかります。
このとき、図2における水面の高さを□cmとおくと、図1・2で水量は変わっていないので、
\(17.5\times18=6\times6\div2\times□\)
より、図2の水面の高さは17.5cmとわかります。
\(\\\) - (2) 水面の高さが7.5cm低くなったことから、残った水の量を求めると、
\(6\times6\div2\times10=180\)
より、180㎠とわかります。
このとき、図1の状態で台形の部分を底面と考えると、
\(\fbox{台形の面積}\times18=180\)
なので、台形の面積は10㎠とわかります。
また、△ABCは小さな二等辺三角形と台形からできているので、小さな二等辺三角形の面積は8㎠とわかります。
ここで、小さな二等辺三角形の1辺の長さを求めると、
\(\fbox{1辺の長さ}\times\fbox{1辺の長さ}\div2=8\)
となり、1辺の長さは4cmとわかります。
以上より、図1の水面の高さは、
\(6-4=2\)
より、2cmとわかります。


