問題
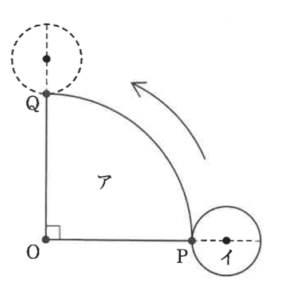
図のように、図形アは点Oを中心とする半径8cmの円の一部です。円イが図形アの周りを滑ることなく転がります。図のPから矢印の向きにQまで円イが転がると、Pで図形アと接していた円イ上の点が、Qで再び図形アに重なります。また、円周率は3.14とします。
- (1) 円イの半径は何cmですか。
- (2) 円イが図形アの周りを1周したとき、円イが通った部分の面積は何㎠ですか。
解説
- (1) 円イの円周の長さが、図形アの弧の長さと等しいので、
\(\fbox{円イの半径}\times2\times3.14=8\times2\times3.14\times\dfrac{1}{4}\)
\(\fbox{円イの半径}=2\)
より、円イの半径は2cmとわかります。
\(\\\) - (2)
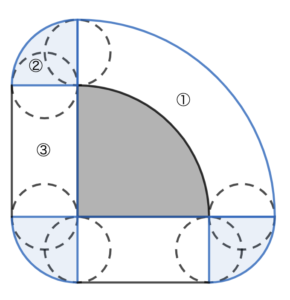
円イが図形アを1周する様子を図に表すと上図のようになります。このとき、円イの通過した部分の面積は、
\(①+②\times3+③\times2\)
と表すことができます。
ここで、①〜③の面積を計算すると、
\(①=12\times12\times3.14\times\dfrac{1}{4}-8\times8\times3.14\times\dfrac{1}{4}\)
\(②=4\times4\times3.14\times\dfrac{1}{4}\)
\(③=4\times8\)
より、求める面積は、
\(12\times3.14+20\times3.14+64\)
\(=164.48\)
となり、164.48㎠とわかります。


