問題
下の図のような双六があり, Aをスタート地点とする. 賽子を振って出た目の数だけコマをゴール地点に向かって進める. この双六には次のようなルールがある.
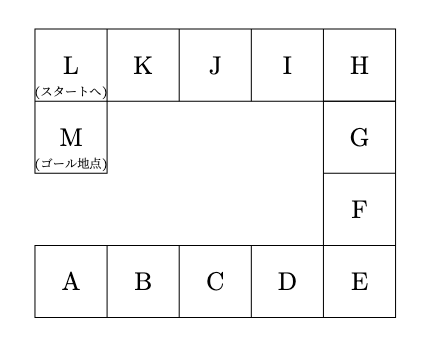
- ルール①
- Mでちょうど止まった場合にのみゴールすることができ, それ以降賽子は振らないものとする.
- ルール②
- Mを超える目が出た場合は, その分だけM(ゴール地点)から戻る.
- 例:Jにいて5の目を出した場合は, J→K→L→M→L→KでKになる.
- Mを超える目が出た場合は, その分だけM(ゴール地点)から戻る.
- ルール③
- Lで止まった場合は直ちにスタート地点に戻される.
- 例:Jにいて4の目を出した場合は, J→K→L→M→LでA(スタート地点)へ戻される.
- Lで止まった場合は直ちにスタート地点に戻される.
次の問に答えなさい.
解説
- (1) 賽子を2回振った後, コマがIにいた. 1回目, 2回目の賽子の目の組合せは何通り考えられるか.
- 2回の最大値は(6,6)で12となるので, Mから折り返してIに着くことや, LからAを経由してIに着くことはないとわかります.
よって, 2回の目の和が8になる場合の数を考えると, (2,6), (3,5), (4,4), (5,3), (6,2)の5通りとなります.
- 2回の最大値は(6,6)で12となるので, Mから折り返してIに着くことや, LからAを経由してIに着くことはないとわかります.
- (2) 賽子をちょうど3回振ったとき, ゴールすることができた. 1回目, 2回目, 3回目の賽子の目の組合せは何通り考えられるか.
- 3回の目の和が12になる組み合わせは, (1,5,6), (2,4,6), (2,5,5), (3,3,6), (3,4,5), (4,4,4)で, それぞれの順列を考えると$3\times6+2\times3+1=25$通りなります.
また, 2回の和が11になる場合はLからAに戻され, (5,6,1)と(6,5,1)はゴールに着かないので, 求める場合の数は23通りになります.
- 3回の目の和が12になる組み合わせは, (1,5,6), (2,4,6), (2,5,5), (3,3,6), (3,4,5), (4,4,4)で, それぞれの順列を考えると$3\times6+2\times3+1=25$通りなります.
- (3) 賽子を4回振った後, コマがFにいた. 1回目, 2回目, 3回目, 4回目の賽子の目の組合せは何通り考えられるか.
- 以下のように場合分けをして考えると,
- ① 初めの2回の目の和が11, 残りの2回の目の和が5になる
初めの2回の目の出方; (5,6)$\times2$
残りの2回の目の出方; (1,4)$\times2$, (2,3)$\times2$
より$2\times4=8$通り - ② 初めの3回の和が11, 残りの1回の目が5になる
初めの3回の目の出方; (1,4,6)$\times6$, (1,5,5)$\times3$, (2,3,6)$\times6$, (2,4,5)$\times6$, (3,3,5)$\times3$, (3,4,4)$\times3$
より27通り - ③ 初めの3回の和が13, 残りの1回の目が5になる
初めの3回の目の出方; (1,6,6)$\times3$, (2,5,6)$\times6$, (3,4,6)$\times6$, (3,5,5)$\times3$, (4,4,5)$\times3$
より21通りで, 2回目で11になる(5,6,1), (6,5,1)と12になる(6,6,1)を除くと, 18通り - ④ 4回の目の和が5になる
(1,1,1,2)$\times4$より4通り
- ① 初めの2回の目の和が11, 残りの2回の目の和が5になる
- となるので, 求める場合の数は57通りになります.
- 以下のように場合分けをして考えると,


