問題
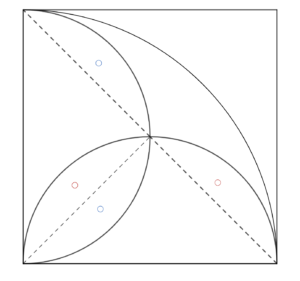
下の図は、1辺の長さが4cmの正方形と扇形を組み合わせたものである。
- (1) AとBの周の長さを求めなさい。
- (2) AとBの面積を求めなさい。
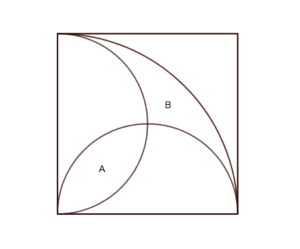
解説
- (1) AとBの周の長さを分解して考えると、半径2cmの半円が2つと、半径4cmの四分円1つに分けられます。
ここで、それぞれの長さを求めると、
\(2\times2\times\pi\times\dfrac{1}{2}\times2+4\times2\times\pi\times\dfrac{1}{4}\)
\(=6\pi\)
より、\(6\pi\)cmとわかります。 - (2) AとBの面積を図のように移動させると、求めたい面積は、半径4cmの四分円から長さ4cmの直角二等辺三角形を引いたものになるので、
\(4\times4\times\pi\times\dfrac{1}{4}-4\times4\times\dfrac{1}{2}\)
\(=4\pi-8\)
より、面積は(\(4\pi-8\))㎠になります。