問題
下の図において, 図形ABEは, Bを中心とした中心角45$^{\circ}$の扇形, 図形ACDは, Cを中心とした中心角45$^{\circ}$の扇形である. このとき, 斜線部分の面積は$\fbox{ }$cm$^{2}$である.
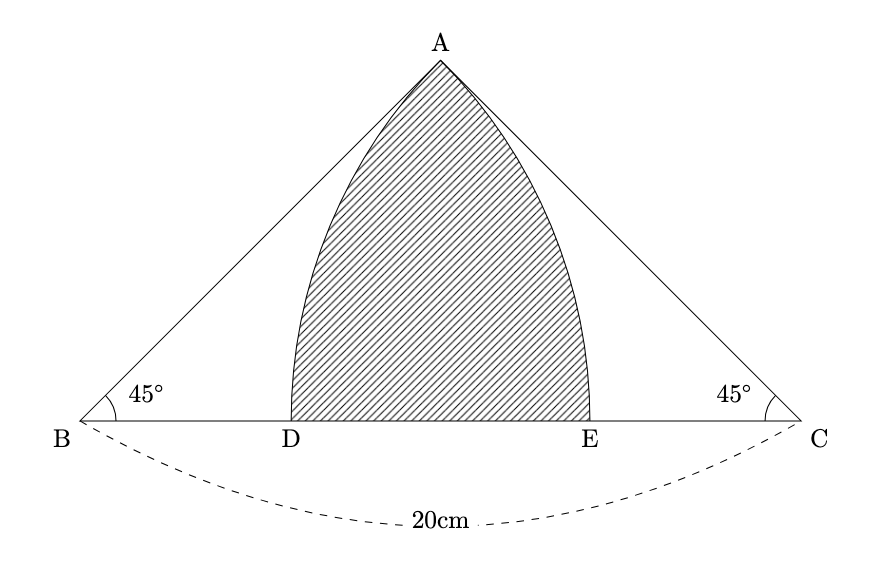
解説
以下のように補助線を引くと,
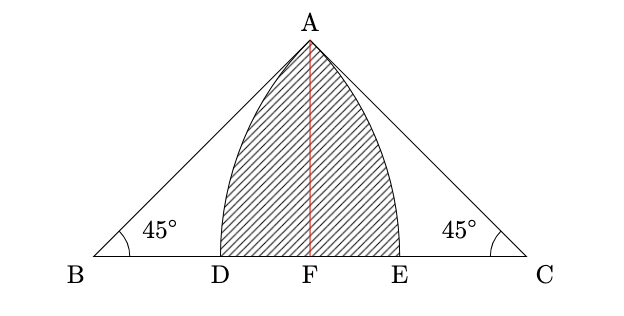
斜線部分の面積の半分は, 半径AC, 中心角45$^{\circ}$の扇形から直角二等辺三角形ACFを引いたものになります.
ここで, $\mathrm{AC}\times\mathrm{AC}\times3.14\times\dfrac{1}{8}-10\times10\div2$より, ACの長さそのものは求められないので, $\mathrm{AC}\times\mathrm{AC}$を考えると, 正方形の面積より, $\mathrm{AC}\times\mathrm{AC}\div2=10\times10=100$から$\mathrm{AC}\times\mathrm{AC}=200$とわかります.
以上から, 求める面積は,
$\bigg(200\times3.14\times\dfrac{1}{8}-10\times10\div2\bigg)\times2=57$より,
$\fbox{ }=$$57(\mathrm{cm}^{2})$となります.


