早稲田佐賀中学校の算数入試問題に挑戦！〜2022年度1月入試〜[大問4-平面図形]

問題

下の図は, ADとBCが並行な台形ABCDであり, 点Eは辺CDの真ん中の点です. 次の問に答えなさい.

解説

• (1)　四角形ABEDと三角形BCDではどちらの面積が大きいか求めなさい. 尚, この問題は, 解答までの考え方を示す式や文章, 図などを書きなさい.
  • $\triangle\mathrm{ABD}:\triangle\mathrm{BCD}=6:14=3:7$, $\triangle\mathrm{BCE}:\triangle\mathrm{BED}=1:1$から, $\triangle\mathrm{ABD}:\triangle\mathrm{BCE}:\triangle\mathrm{BED}=6:7:7$より, $\Box\mathrm{ABED}:\triangle\mathrm{BCD}=13:14$となるので, 三角形BCDの方が面積が大きいとわかります.
• (2)　ACとBD, BEとの交点をそれぞれF, Gとします.
  
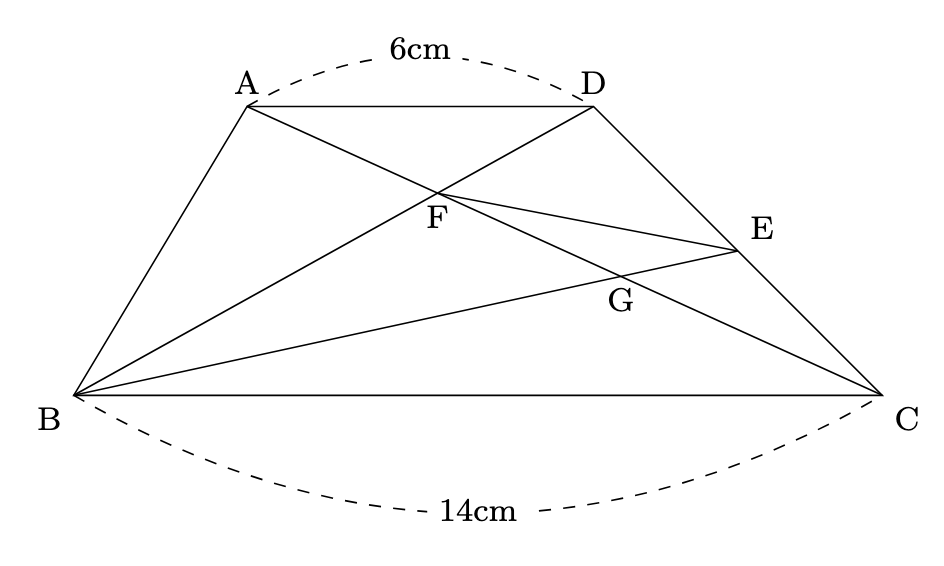
  • ①　三角形BCFと台形ABCDの面積の比を求めなさい.
    • $\mathrm{AD}\parallel\mathrm{BC}$から, $\triangle\mathrm{ABF}:\triangle\mathrm{FBC}=\mathrm{AF}:\mathrm{FC}=\mathrm{AD}:\mathrm{BC}=6:14=3:7$より, 台形ABCDの面積を$\fbox{1}$と置くと, $\triangle\mathrm{BCF}=\fbox{1}\times\dfrac{14}{6+14}\times\dfrac{7}{3+7}=\fbox{0.49}$より, $\triangle\mathrm{BCF}:\Box\mathrm{ABCD}=$$49:100$となります.
  • ②　三角形EFGと三角形BCGの面積の比を求めなさい.
    • 以下のようにEからBCに平行な補助線を引くと,
      
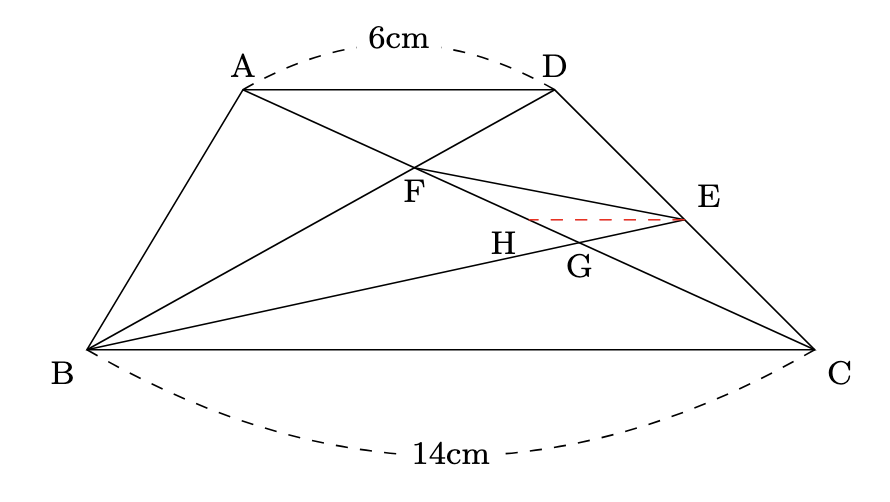
      $\mathrm{HE}=6\times\dfrac{1}{1+1}=3\mathrm{cm}$なので, $\mathrm{BG}:\mathrm{GE}=3:14$から, 台形ABCDの面積を$\fbox{1}$と置くと, $\triangle\mathrm{EFG}=\fbox{1}\times\dfrac{14}{6+14}\times\dfrac{1}{1+1}\times\dfrac{7}{3+7}\times\dfrac{3}{14+3}$, $\triangle\mathrm{BCG}=\fbox{1}\times\dfrac{14}{6+14}\times\dfrac{1}{1+1}\times\dfrac{14}{3+14}$より, $\triangle\mathrm{EFG}:\triangle\mathrm{BCG}=\dfrac{3}{20}:1=$$3:20$となります.