問題
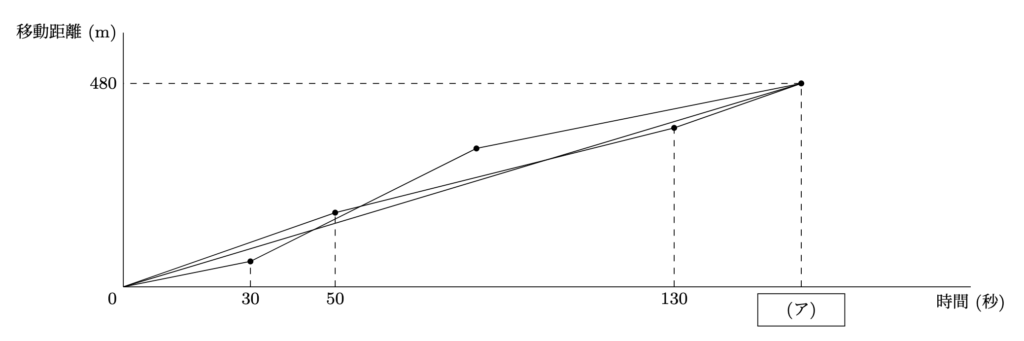
A君, B君, C君は, 同時に駅を出発して480m先にある学校へ向かった. 下のグラフは, 3人が出発してからの時間と, 移動距離の関係を表したものである. 3人が学校に到着するまでにかかった時間は$\fbox{ (ア) }$秒である. また, A君は秒速3.5m, $\fbox{ (イ) }$m, 3.5mと2回速さを変え, B君は秒速2m, 5m, 2mと2回速さを変え, C君は秒速3mの一定の速さで走った. 次の問に答えよ.
解説
- (1) $\fbox{ (ア) }$・$\fbox{ (イ) }$に当てはまる数を求めよ.
- C君に注目すると, 480mの距離を秒速3mで走ったので, $480\div3=160$より, $\fbox{ (ア) }$=160(秒)とわかります.
- 次に, A君に着目すると, 秒速3.5mで走ったのは$50+(160-130)=80$秒なので, 秒速$\fbox{ (イ) }$mで走った時間も$160-80=80$秒とわかります. 以上より, $\fbox{ (イ) }\times80=480-(3.5\times80)$から, $\fbox{ (イ) }$=2.5(m)となります.
- (2) B君が, 秒速5mの速さで走っていた時間を求めよ.
- 以下のように, 面積図を考えると,
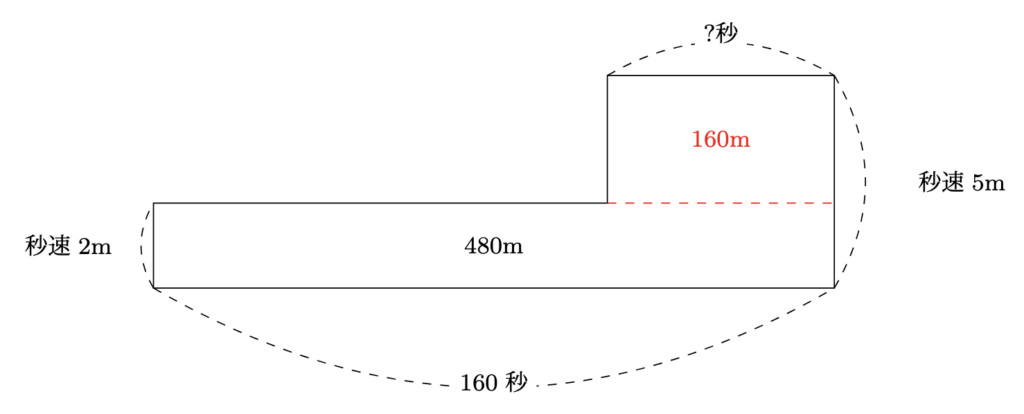
$?=(480-2\times160)\div(5-2)=53\dfrac{1}{3}$より, $53\dfrac{1}{3}$秒となります.
- 以下のように, 面積図を考えると,
- (3) B君がA君を追い越すのは, 同時に出発してから何秒後かを求めよ.
- 進行グラフを見ると, B君がA君を追い越すのは50秒を少し過ぎたところとわかるので, 50秒の時点での両者の距離を求めると,
- A君の移動距離; $3.5\times50=175$m
- B君の移動距離; $2\times30+5\times(50-30)=160$m
- から, $175-160=15$mより, 追い越し算を考えると, $15\div(5-2.5)=6$秒後となるので, 出発してからは56秒後とわかります.
- 進行グラフを見ると, B君がA君を追い越すのは50秒を少し過ぎたところとわかるので, 50秒の時点での両者の距離を求めると,


