問題
図のような直角三角形ABCがあります. 辺ABの真ん中の点をD, ADの真ん中の点をEとします. 点Eを通り辺BCに平行な直線と, 辺ACとの交わる点をFとし, FCの真ん中の点をGとします. また, 2点EとC, DとGをそれぞれ結び, ECとDGの交わる点をHとします. 次の問に答えなさい.
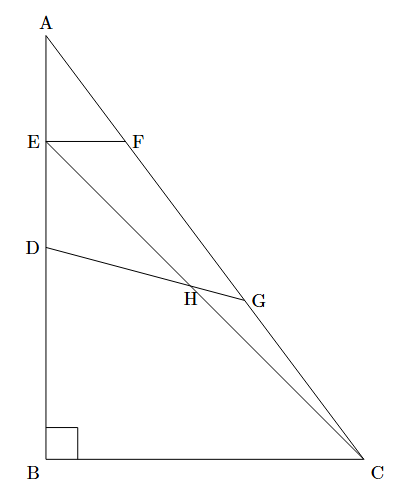
解説
(1) AFとFGの長さの比を求めなさい.
$\mathrm{AE}:\mathrm{EB}=\mathrm{AF}:\mathrm{FC}=1:3$,
$\mathrm{FG}:\mathrm{GC}=1:1$
より,
$\mathrm{AF}:\mathrm{FG}=$$2:3$
となります.
(2) EHとHCの長さの比を求めなさい.
以下のように補助線を引き, P, Qの位置を定めると,
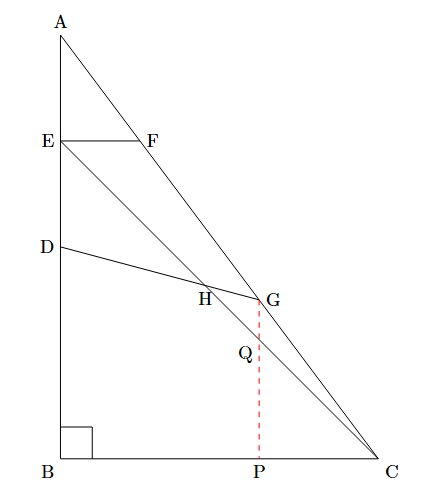
$\mathrm{GQ}:\mathrm{AE}=\mathrm{CG}:\mathrm{CA}=3:8$
より,
$\mathrm{GQ}:\mathrm{ED}=\mathrm{QH}:\mathrm{HE}=3:8$.
また,
$\mathrm{CQ}:\mathrm{QE}=\mathrm{CG}:\mathrm{GA}=3:5$
より,
$\mathrm{EH}:\mathrm{HC}=$$5:6$
となります.
(3) DHとHGの長さの比を求めなさい.
$\mathrm{ED}:\mathrm{GQ}=\mathrm{DH}:\mathrm{HG}=$$8:3$
*(2)の途中で(3)が求められる不思議なパターン(設問順に解けるより良い方法があるかもしれません)

