問題
下の図のように, 対角線の長さが10cmの正方形の色紙を一直線になるように繋げて飾りを作ります. このとき, 糊代の部分が「対角線の長さが4cmの正方形」になるようにします. 例えば下の図のように, 色紙を2枚繋ぐと, 飾り全体の長さは16cm, 飾り全体の面積は92cm$^{2}$になります. 色紙を3枚繋ぐと, 飾り全体の長さは22cmになります. このとき, 次の問に答えなさい.
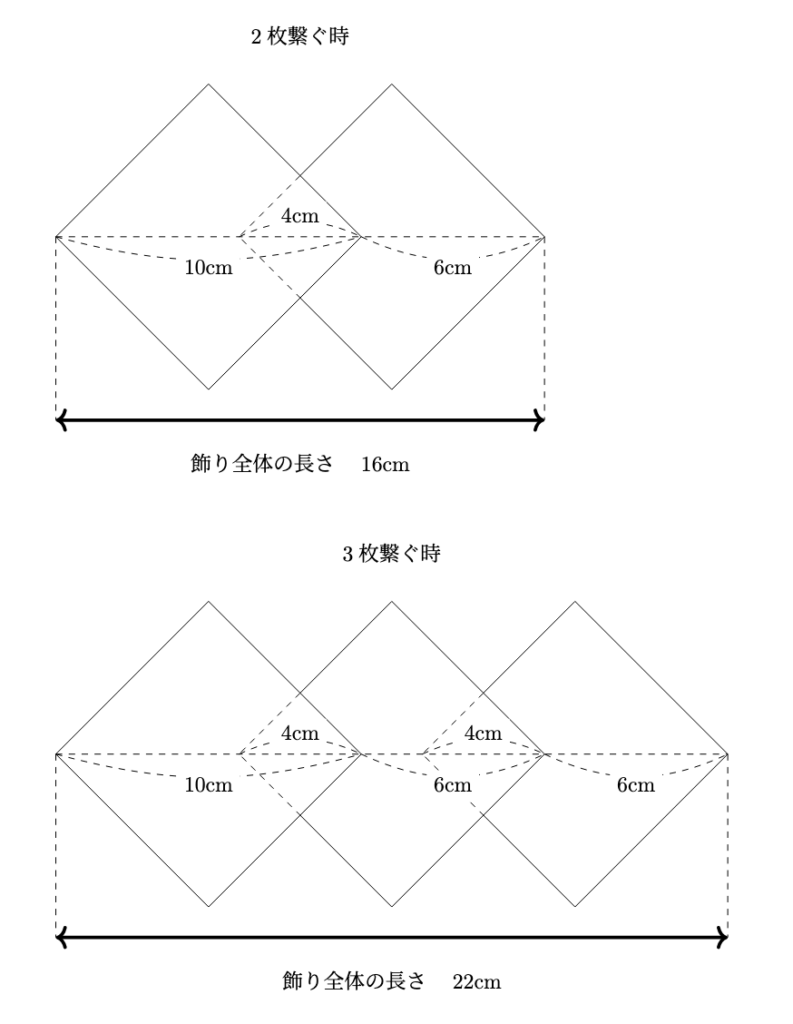
解説
- $(1)$ 色紙を5枚繋ぐと, 飾り全体の長さは何cmになりますか.
- 色紙を1枚増やすと6cm長くなるので, 5枚では, $10+6\times(5-1)=$$34\mathrm{cm}$となります.
- $(2)$ 色紙を5枚繋ぐと, 飾り全体の面積は何cm$^{2}$になりますか.
- 色紙を1枚増やすと, 面積は$10\times10\div2-4\times4\div2=42\mathrm{cm}^{2}$増えるので, 5枚では, $50+42\times(5-1)=$$218\mathrm{cm}^{2}$となります.
- $(3)$ 飾り全体の面積が638cm$^{2}$のとき, 色紙を何枚繋ぎましたか.
- (2)の逆をすればよいので,
$50+42\times(\square-1)=638$
$42\times(\square-1)=638-50$
$\square-1=14$
$\square=$$15\mbox{枚}$となります.
- (2)の逆をすればよいので,


