問題
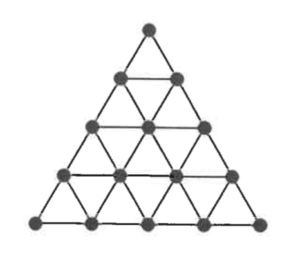
同じ長さの棒と粘土玉を使って、何段かの正三角形を作ります。下の図は、4段の正三角形を表しています。
- (1) Aさんが何段かの正三角形を作ったところ、棒が4本出ている粘土玉が18個ありました。
- ① Aさんは何段の正三角形を作りましたか。
- ② Aさんが使った棒は全部で何本ですか。
- (2) Bさんが何段かの正三角形を作ったところ、棒が6本出ている粘土玉が36個ありました。Bさんが使った粘土玉は全部で何個ですか。
解説
- (1)①
まずは、各段で棒が4本出ている粘土玉が何個あるかを数えると、

のようになります。
以上より、粘土玉が18個になっているのは、正三角形が7段のときになります。
*\(\fbox{個数}=3\times(\fbox{段数}-1)\)という関係式を用いても問題ありません。
\(\\\) - (1)②
今度は、各段における棒の本数を数えると、

のようになります。
以上より、正三角形が7段のときの、棒の本数は84本になります。
*\(\fbox{本数}=(1+\fbox{段数})\times\fbox{段数}\div2\)という関係式を用いても問題ありません。
\(\\\) - (2)
各段で棒が6本出ている粘土玉が何個あるかを数えると、

のようになり、36個なのは、正三角形が10段のときとわかります。
また、正三角形が10段のときの粘土玉の個数を数えると、
より、66個とわかります。
*\(\fbox{個数}=(\fbox{段数}+2)\times(\fbox{段数}+1)\div2\)という関係式を用いても問題ありません。


