問題
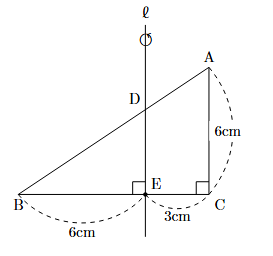
図のように直角三角形ABCと直線ℓが2点D, Eで交わっています. 直角三角形ABCを直線$\ell$の周りに1回転させてできる立体の体積を求めなさい. 但し, 円錐の体積は(底面積)$\times$(高さ)$\div3$で求めるものとします.
解説
以下のように回転体を考えると,
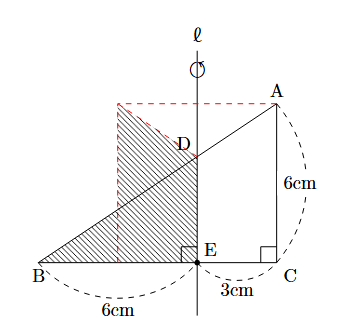
求める体積は, 斜線部を回転させたものだとわかるので,
$6\times6\times3.14\times6\times\dfrac{2}{3}\times\dfrac{1}{3}+3\times3\times3.14\times4-3\times3\times3.14\times2\times\dfrac{1}{3}\times2$
$=(48+36-12)\times3.14$
$=$$226.08\mathrm{cm}^3$
となります.

