問題
姉と弟は毎週日曜日の午前10時に, 家から5km離れた図書館へ一緒に向かう. 2人で一緒に歩くときは, 時速4kmで向かう. 弟が忘れ物に気付いた場合は, 時速8kmで一人で家に戻り更に姉を追いかける. その間, 姉は時速2kmで図書館へ向かう. 次の問に答えよ. 但し, 家で忘れ物を探す時間は考えないものとし, 忘れ物を取りに帰るのは1回とする.
解説
- (1) 5月のある日曜日, 弟が忘れ物をすることなく, 2人は一緒に図書館へ到着した. 2人が到着した時刻を求めよ.
- 5km離れた図書館へ時速4kmで向かうので, $5\div4=1.25$(時間)より, 到着する時間は11時15分となります.
- (2) 10月のある日曜日, 弟が家から2kmのところで忘れ物に気付いた. 2人が一緒に図書館に到着した時刻を求めよ. 尚, この問題は, 解答までの考え方を示す式や文章, 表などを書け.
- 以下のように, 進行グラフを描くと,$\\$
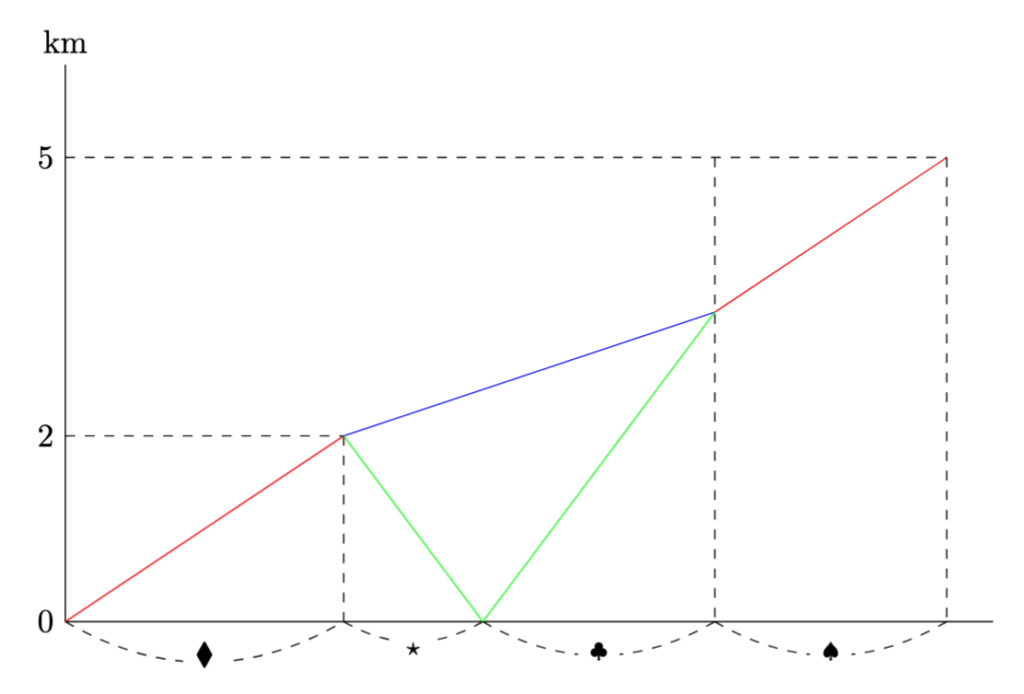
姉と弟が2km進むのにかかる時間は, $\blacklozenge=2\div4=\dfrac{1}{2}$時間, 弟が2kmを引き返す時間は, $\star=2\div8=\dfrac{1}{4}$(時間)になります.
$\\$
次に, 弟が姉に追いつく時間を考えると, 出発してから45分の時点で姉は$2+2\times\dfrac{45-30}{60}=2.5$kmなので, $(\clubsuit=)2.5\div(8-2)=\dfrac{5}{12}$時間とわかります.
$\\$
最後に, 弟が姉に追いついてから図書館に着くまでの時間を考えると, $(\spadesuit=)(5-8\times\dfrac{5}{12})\div4=\dfrac{5}{12}$時間となります.
$\\$
以上より, かかった時間の合計は, $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{5}{12}+\dfrac{5}{12}=\dfrac{19}{12}$時間となるので, 到着時刻は11時35分となります.
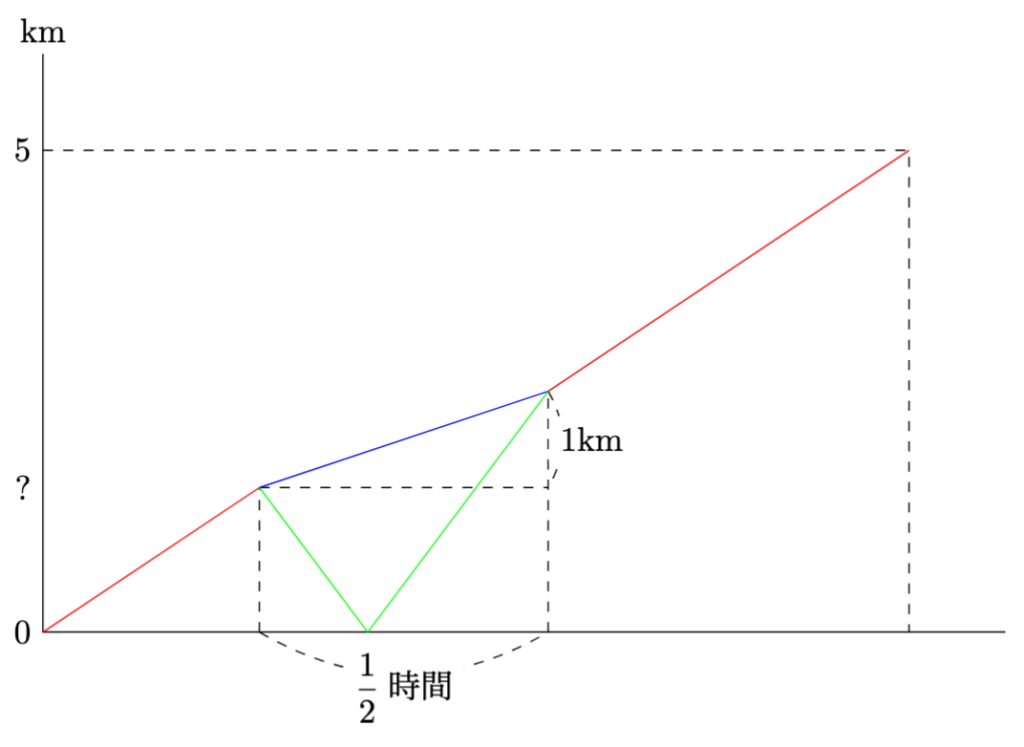
- 以下のように, 進行グラフを描くと,$\\$
- (3) 12月のある日曜日, 図書館へ向かう途中で, 弟が忘れ物に気付いた. 出発してから2人が一緒に歩いた時間の合計は1時間であり, 2人は一緒に図書館へ到着した. 弟は家から何kmのところで忘れ物に気付いたか求めよ.
- 2人が一緒に歩いた距離が$4\times1=4$kmなので, 姉が1人で歩いた距離は$5-4=1$kmで, 時間は$1\div2=\dfrac{1}{2}$時間とわかります.
$\\$
また, この間に弟が移動した距離は, $8\times\dfrac{1}{2}=4$kmなので, 引き返した場所は家から$(4-1)\div2=1.5$より, 1.5kmのところとなります.
- 2人が一緒に歩いた距離が$4\times1=4$kmなので, 姉が1人で歩いた距離は$5-4=1$kmで, 時間は$1\div2=\dfrac{1}{2}$時間とわかります.


