早稲田佐賀中学校の算数入試問題に挑戦！〜2024年度1月入試〜[大問5-空間図形と水量]

問題

底面の半径が6cm, 高さが18cmの円錐状の容器に水が入っている. 次の問に答えなさい.

解説

• (1)　この容器の容積を求めなさい.
  • $6\times 6\times 3.14\times 18÷3=$$678.24{\mathrm{cm}}^3$
• (2)　次のそれぞれの場合において, 入っている水の体積を求めなさい.
  • (i)　この容器の底面を下にして置いたところ, 水面の高さが12cmになった.
    
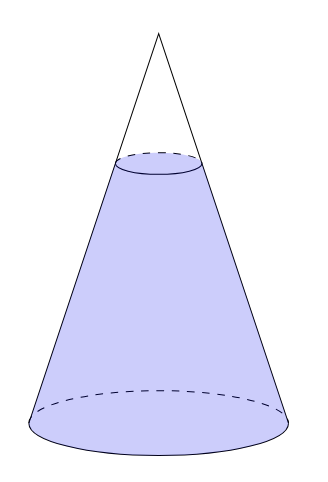
    • 小さな円錐と大きな円錐の体積比を考えると, 相似比$12:18=2:3$より, $8:27$となり, 円錐台の体積は大きな円錐の${\displaystyle \frac{19}{27}}$倍とわかります.
      以上より, 求める体積は,
      $6\times 6\times 3.14\times 18÷3\times {\displaystyle \frac{19}{27}}=$$653.12{\mathrm{cm}}^3$となります.
  • (ii)　この容器を図のように傾けたとき, 水面が容器の頂点を通り, 底面の一部が水に触れている. 底面の中心はOで, 図の角Oは直角となった. 尚, この問題は解答までの考え方を示す式や文章を書いて答えなさい.
    
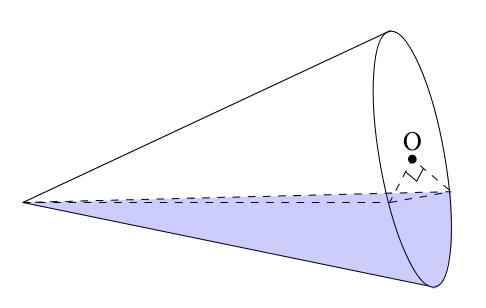
    • 立体の形状を考えると, 高さが18cmの錐体となるので, 体積を求めるためには, 底面積が必要となります.
      ここで, 以下のように底面積を考えると,
      
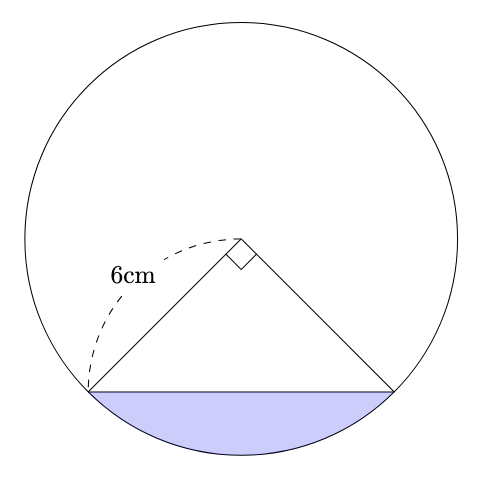
      $6\times 6\times 3.14\times {\displaystyle \frac{1}{4}}-6\times 6\times {\displaystyle \frac{1}{2}}=10.26{\mathrm{cm}}^2$とわかるので,
      求める体積は, $10.26\times 18÷3=$$61.56{\mathrm{cm}}^3$となります.