問題
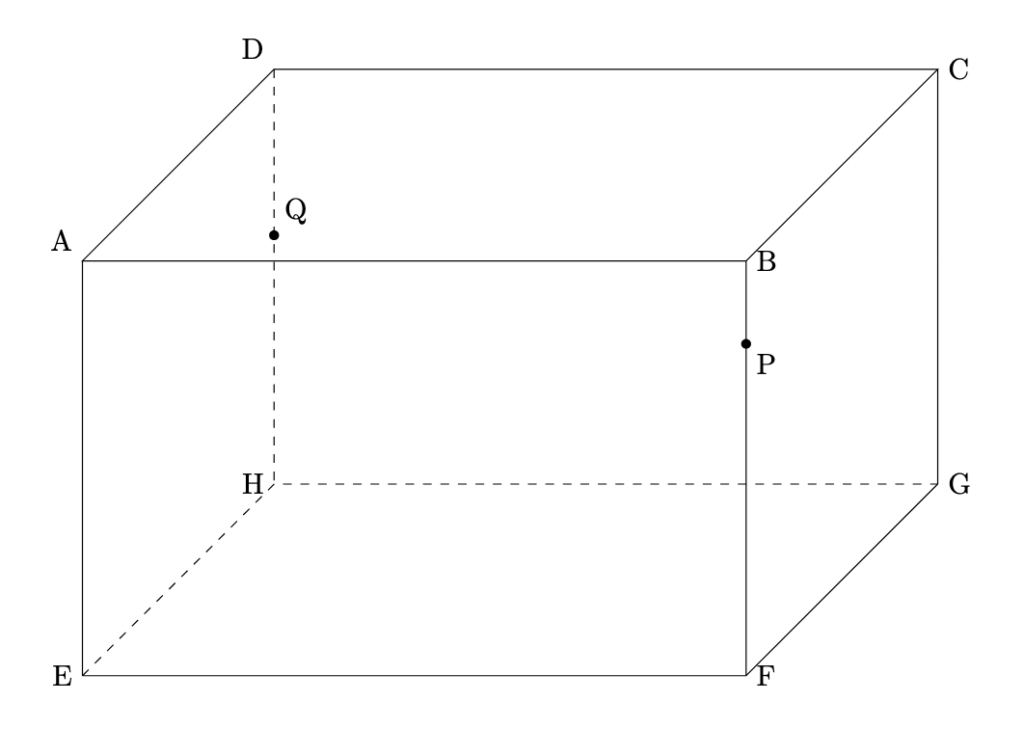
下の図のような, $\mathrm{AB}=8\mathrm{cm}$, $\mathrm{BF}=\mathrm{BC}=6\mathrm{cm}$の直方体があります. この直方体の辺BF上に$\mathrm{BP}=2\mathrm{cm}$となる点Pと辺DF上に$\mathrm{DQ}=\mathrm{QH}$となる点Qをとります. このとき, 次の問に答えなさい.
解説
- (1) この直方体の体積を求めなさい.
- $8\times6\times6=288$より$288\mathrm{cm}^{3}$となります.
- (2) この直方体を3点C, P, Qを通る平面で切ったとき, 点Aを含む方の立体の体積を求めなさい.
- 立体の切断面を図に表すと,
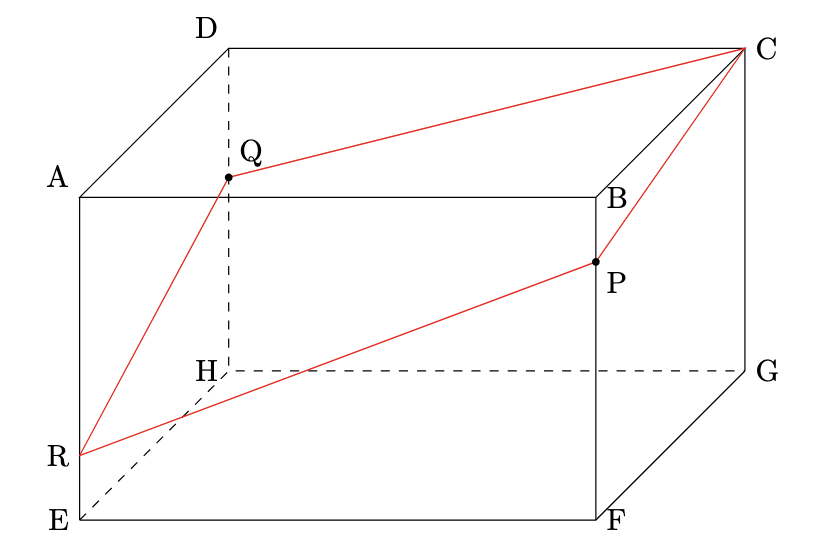
ARの長さは5cmなので, 点Aを含む方の立体は, 底面積が$8\times6=48\mathrm{cm}^{2}$, 平均の高さが$(2+0+3+5)\div4=2.5\mathrm{cm}$の直方体になるので, 体積は$48\times2.5=120$より, $120\mathrm{cm}^{3}$となります.
- 立体の切断面を図に表すと,
- (3) (2)の立体を更に平面ACGEで切ったとき, 点Bを含む方の立体の体積を求めなさい.
- (2)同様, 立体の切断面を図に表すと,
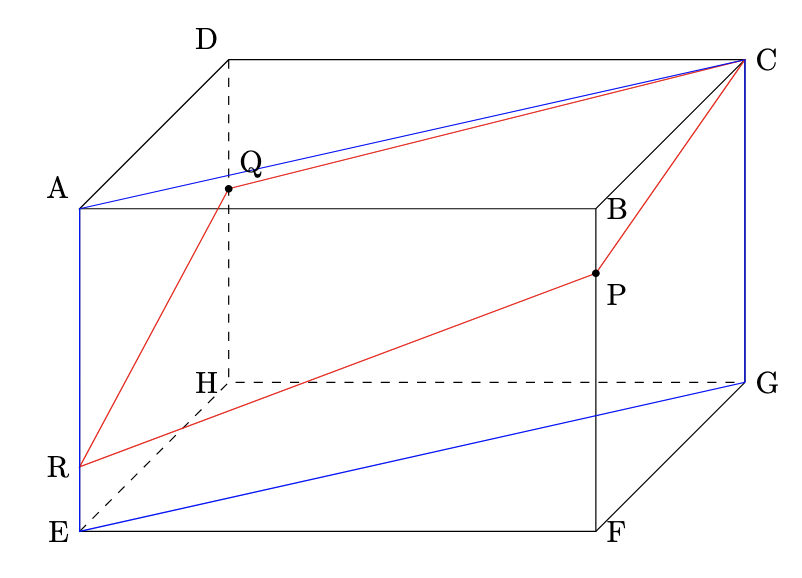
点Bを含む方の立体は, 底面積が$(2+5)\times8\div2=28\mathrm{cm}^{2}$, 高さが6cmの四角錐になるので, 体積は$28\times6\div3=56$より, $56\mathrm{cm}^{3}$となります.
- (2)同様, 立体の切断面を図に表すと,


