問題
AさんとBさんは, 「一つの円に何本かの直線を引いて, 円が何個の図形に分けられるか」という問題を考えています.
解説
- (1) 以下の「先生」, 「Aさん」, 「Bさん」の会話文を読み◻︎に当てはまる数字を答えなさい. 但し, 同じ記号の◻︎には同じ数字が入るものとします.
- 先生:
今, 直線は次の3つの条件を満たしているものとします.
\begin{equation*}
\begin{cases}
\mbox{① 直線の両端は円上にある.}\\
\mbox{② どの2本の直線も平行ではなく, 円の内側で交わっている.}\\
\mbox{③ どの3本の直線も1点で交わらない.}
\end{cases}
\end{equation*}
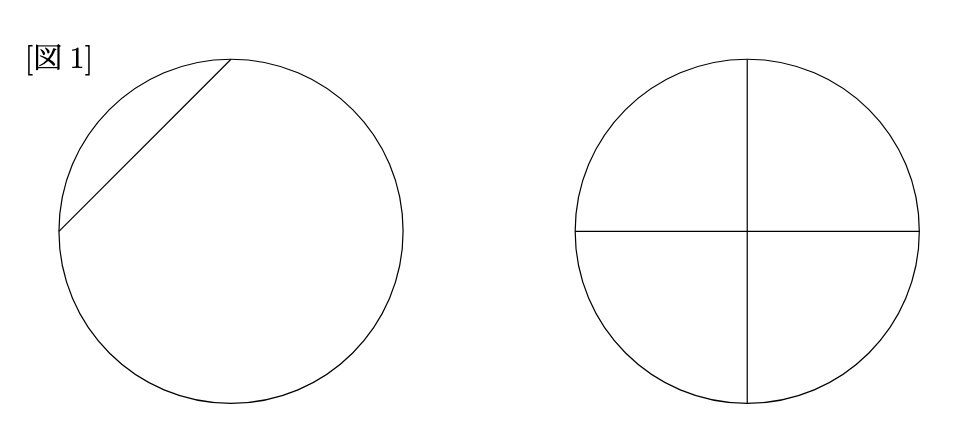
[図1]のように直線を1本引いてみると円は2個の図形に, 直線を2本引くと円は4個の図形に分けられます.
それでは3本の直線を引いたとき, 円は何個の図形に分けられますか.
 Aさん:$\fbox{ (ア) }$個に分けられます.
Aさん:$\fbox{ (ア) }$個に分けられます.
先生:そうですね. では, 直線の本数を増やしていき10本になったらどうなるでしょうか.
Bさん:直線が多くて, 図が描けません.
先生:
図を描くのは難しいですね. そこで実際に直線を10本引くのではなく, 別の方法で数えることを考えてみましょう.
今, 円に何本か直線が引かれていて, 何個かの図形に分けられていたとします. そこに, 3つの条件を満たす直線を1本引いてみます. まず, 円上に1点をとって, そこから新しい直線を少しずつ引いていきます. すると, この直線は既に描かれている直線のどれか1つにぶつかるはずです. このとき図形の個数はどう変化しますか.
Bさん:直線を引く前の図形の個数から$\fbox{ (イ) }$個増えるはずです.
先生:そうです. この性質がポイントです.
Aさん:
そうか. 新しく直線を引いていくと, 前に描かれた直線にぶつかる. その度に図形の個数が$\fbox{ (イ) }$個ずつ増えていく. これを円上の点に辿り着くまで行うのですね.
Bさん:
それなら, 円に描き入れた直線の本数と分けられた図形の個数を表にすれば, 図形の個数を順番に埋めていけるね. えーと, 10本の直線で円は$\fbox{ (ウ) }$個の図形に分けられることがわかりました.
先生:正解です. よくできましたね. それでは, 次の問題はどうでしょうか.- 3本直線を引くと, 例えば以下のような形になるため,
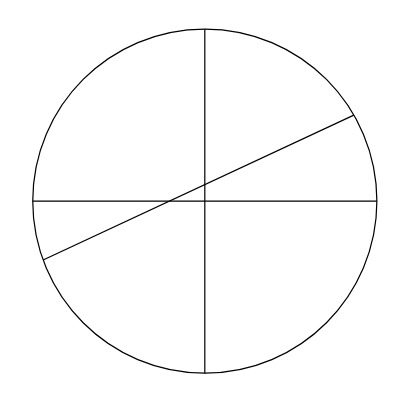
領域を数えると, (ア)=7(個)になります. - また, 直線が既存の直線と交わることで増える図形は, (イ)=1(個)なので, 10本の直線を引いた場合は, $2+2+3+4+5+6+7+8+9+10=56$より, (ウ)=56(個)の図形に分けられます.
- 3本直線を引くと, 例えば以下のような形になるため,
- 先生:
<問題>
12本の直線で円が何個かの図形に分けられています. この12本の直線には3本だけ平行な直線が含まれています. 直線は, 平行でないどの2本も円の内側で交わり, どの3本も1点で交わることはありません.
このとき, 円は何個の図形に分けられているでしょうか.
- (2) 上の問題を解きなさい. 尚, この問題は, 解答までの考え方を示す式や文章, 表などを書いて答えなさい.
- 最初に平行な直線3本を引くと, 円は4個の図形に分けられます.
また(1)より, 4本目の直線を引くと, 図形は4個増え, その後は5個, 6個, …, 12個と増えます.
以上より, 円は, $4+4+5+6+7+8+9+10+11+12=76$から, 76個の図形に分かれます.
- 最初に平行な直線3本を引くと, 円は4個の図形に分けられます.


