問題
下の図において, 正三角形ABCのそれぞれの辺の真ん中の点をD, E, Fとし, 辺ABの長さを$7:1$に分ける点をPとする. 点Pを通り, 三角形FBDの面積を2等分する直線を引き, FD, ED, ECとの交点をそれぞれQ, R, Sとする. 次の問に答えよ.
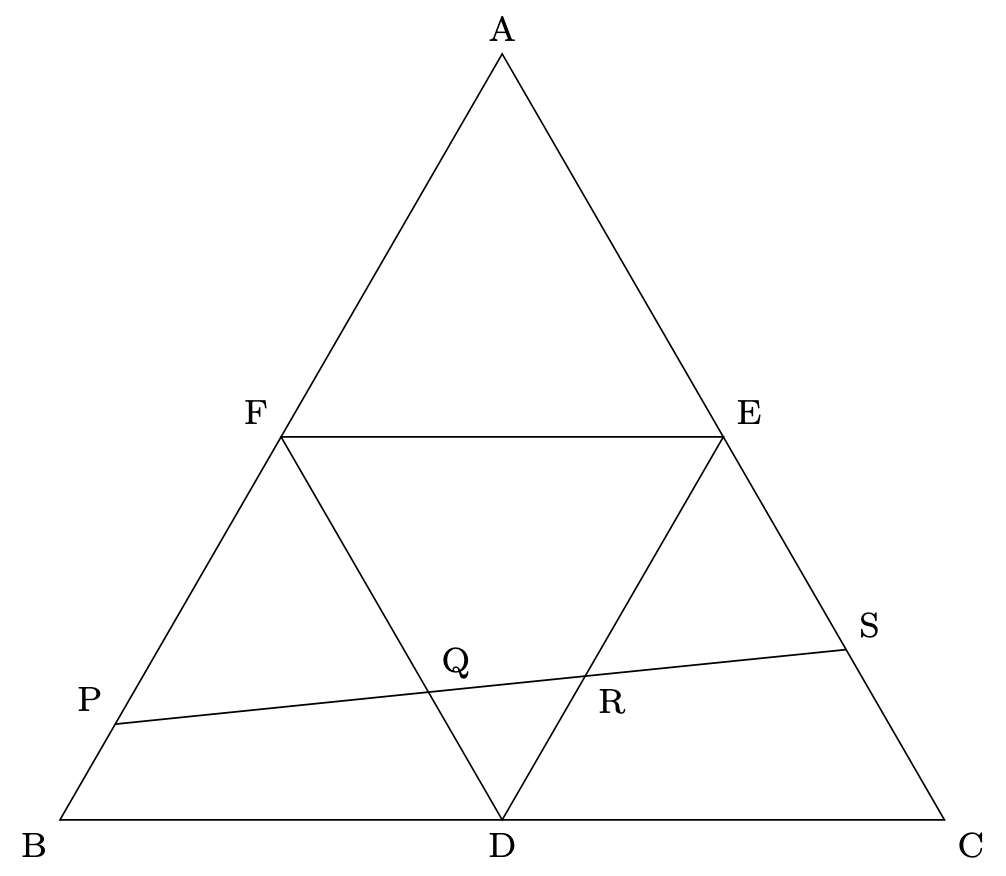
解説
- (1) FQとQDの長さの比を求めよ.
- $\mathrm{AF}:\mathrm{FB}=1:1$, $\mathrm{AP}:\mathrm{PB}=7:1$から, $\mathrm{FP}:\mathrm{PB}=3:1$とわかります.
- また, $\triangle\mathrm{FPQ}=\triangle\mathrm{FBD}\times\dfrac{1}{2}=\triangle\mathrm{FBD}\times\dfrac{\mathrm{FQ}}{\mathrm{FQ}+\mathrm{QD}}\times\dfrac{3}{3+1}$から, $\dfrac{\mathrm{FQ}}{\mathrm{FQ}+\mathrm{QD}}=\dfrac{2}{3}$より,
- $\mathrm{FQ}:\mathrm{QD}=2:1$となります.
- (2) ASとSCの長さの比を求めよ.
- AB//EDより, $\triangle\mathrm{FPQ}$と$\triangle\mathrm{DRQ}$は相似形であることがわかるので, $\mathrm{FQ}:\mathrm{QD}=\mathrm{FP}:\mathrm{RD}=2:1$となります.
- ここで, $\mathrm{FB}=\mathrm{ED}$より, $\mathrm{DR}:\mathrm{RE}=1.5:2.5=3:5$なので, QDの長さを③とおくと, ESの長さは⑤, AEの長さは(FDと同じ長さなので)⑨, SCの長さは④より, ${\mathrm{AS}:\mathrm{SC}}=(9+5):4=7:2$から, $7:2$となります.
- (3) 三角形ABCと三角形QDRの面積の比を求めよ.
- $\triangle\mathrm{QDR}=\triangle\mathrm{FDE}\times\dfrac{\mathrm{QD}}{\mathrm{FQ}+\mathrm{QD}}\times\dfrac{\mathrm{DR}}{\mathrm{DR}+\mathrm{RE}}=\triangle\mathrm{FDE}\times\dfrac{1}{3}\times\dfrac{3}{8}=\triangle\mathrm{FDE}\times\dfrac{1}{8}$
- $\triangle\mathrm{ABC}=\triangle\mathrm{FDE}\times4$
- より, $\triangle\mathrm{QDR}$の面積を①とおくと, $\triangle\mathrm{ABC}$の面積は㉜となるので, 両者の比は$32:1$とわかります.


