問題
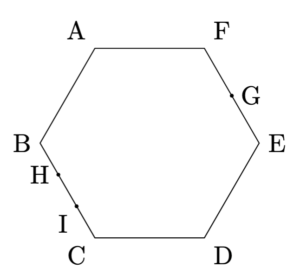
下の図のように, 面積が72cm$^{2}$である正六角形ABCDEFがある. 点Gは辺EFの真ん中の点であり, 点Hと点Iは辺BCを3等分する点である. 次の問に答えよ.
解説
- (1) 三角形BIFの面積を求めよ.
- 以下のように補助線を引くと,
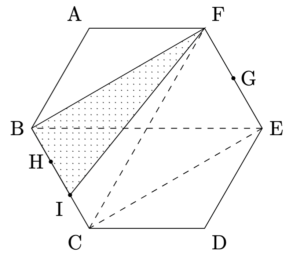
四角形ABCFの面積が36cm$^{2}$, 三角形ABFの面積が12cm$^{2}$なので, 三角形BFIの面積は, $24\times\dfrac{2}{3}=16$より, 16cm$^{2}$となります.
- 以下のように補助線を引くと,
- (2) EIとGIの交点をPとするとき, 五角形CDEPIの面積を求めよ.
- 以下のように補助線を引くと,
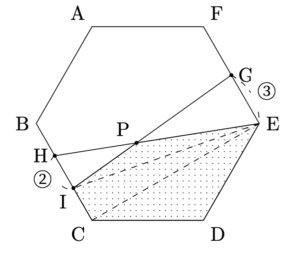
$\mbox{五角形CDEPI}=\mbox{三角形PIE}+\mbox{三角形CEI}+\mbox{三角形CDE}$と分けることができるので, それぞれの面積を求めると,
$\mbox{三角形PIE}=\mbox{三角形GIE}\times\dfrac{2}{2+3}=12\times\dfrac{2}{5}=4.8$cm$^{2}$
$\mbox{三角形CEI}=24\times\dfrac{1}{3}=8$cm$^{2}$
$\mbox{三角形CDE}=12$cm$^{2}$より, 五角形CDEPIの面積は24.8cm$^{2}$になります.
- 以下のように補助線を引くと,
- (3) BEとGHの交点をX, BEとGIの交点をYとするとき, 三角形GXYの面積を求めよ.
- 以下のように補助線を引くと,
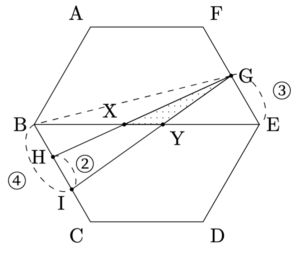
$\mbox{三角形GXY}=\mbox{三角形GXE}-\mbox{三角形GYE}$と分けることができるので, それぞれの面積を求めると,
$\mbox{三角形GXE}=12\times\dfrac{3}{2+5}=\dfrac{36}{5}$cm$^{2}$
$\mbox{三角形GYE}=12\times\dfrac{3}{3+4}=\dfrac{36}{7}$cm$^{2}$より, 三角形GXYの面積は$\dfrac{72}{35}\mbox{cm}^{2}$となります.
- 以下のように補助線を引くと,


