早稲田佐賀中学校の算数入試問題に挑戦！〜2021年度1月A日程〜[大問1-(9)仕事算と鶴亀算の複合問題]

問題

ある仕事を終えるのに, 兄1人だとちょうど27日, 弟1人だとちょうど45日かかる. 2人が一緒に作業をすると, 兄は弟の指示をしながら作業をするため, 兄の作業の速さは10\%遅くなるが, 弟の作業の速さは50\%速くなる. この仕事を, 初めは弟が1人で◻︎日間作業し, その後, 兄と弟が一緒に作業をしたところ, 21日間でちょうど作業を終えることができた.

解説

全体の仕事量を, 27と45の最小公倍数である$\boxed{\text{135}}$と置くと, 兄は1日に$\boxed{\text{5}}$, 弟は1日に$\boxed{\text{3}}$の仕事をすることになります.

また, 2人で一緒に作業する場合, 兄は1日に$5\times (1-0.1)=4.5$より$\boxed{\text{4.5}}$, 弟は1日に$3\times (1+0.5)=4.5$より$\boxed{\text{4.5}}$の仕事をすることになります.

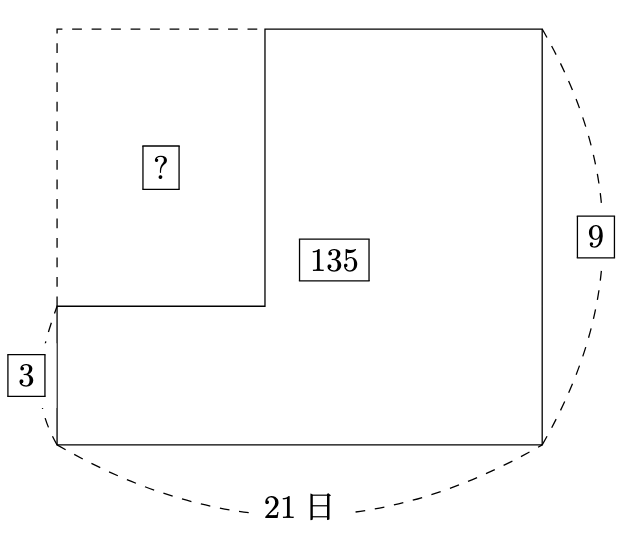
ここで, 弟1人と兄・弟2人が21日間で$\boxed{\text{135}}$の仕事をしたと考えて面積図を作ると, $\boxed{\text{?}}=21\times \boxed{\text{9}}-\boxed{\text{135}}=\boxed{\text{54}}$から, 弟1人が仕事をした日数は$\boxed{\text{54}}÷(\boxed{\text{9}}-\boxed{\text{3}})=9$より, 9日となります.