問題
二人の会話と図より, 次の問に答えなさい。但し, 円周率は3.14とする。また, 解答は答えのみでよい。
- たろう 「運動会のリレーって楽しいよね。」
- はなこ 「わかる!走っていると生きてるって感じがする。」
- たろう 「ちょっとそれはわからないけど・・・。図が僕たちの運動会のフィールドトラックだよ。レーンの幅は1mだよ。」
- はなこ 「内側のレーンを走る人の距離って何mなのかな?」
- たろう 「計算してみようよ。」
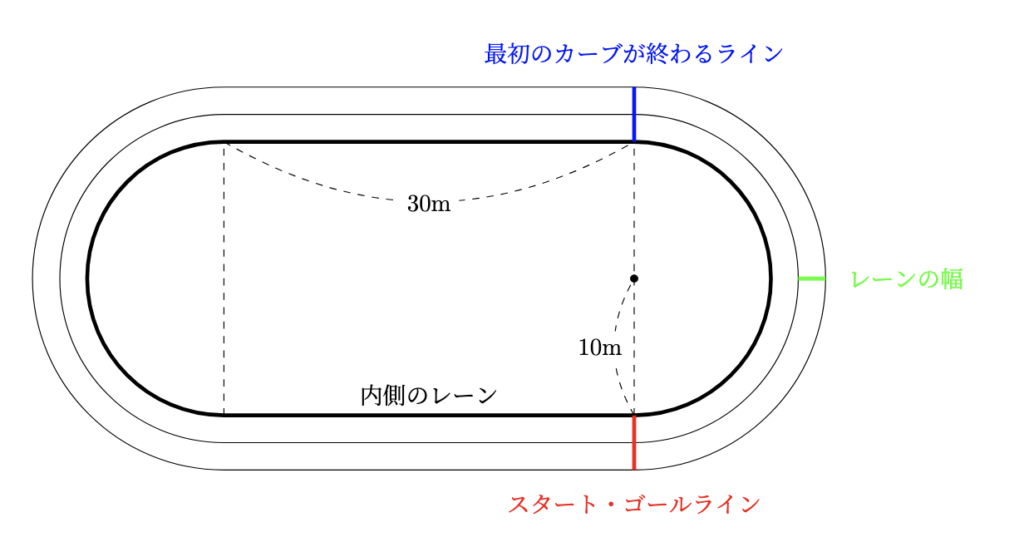
解説
- $(1)$ 図の内側のレーンで走るとき, 1周分の距離を求めなさい。但し, 走る距離は内側の線の長さと同じとする。
- $10\times2\times3.14\times\dfrac{1}{2}\times2+30\times2=122.8$より122.8mとなります.
- たろう 「ところで, 世界陸上見た?」
- はなこ 「見たよ。私は4$\times$400mリレーが好きだな!花形って感じ。」
- たろう 「かっこいいよね。4$\times$400mリレーって第1走者はセパレートコース(スタートしたレーンと同じレーン)を走るんだけど, 第2走者が最初のカーブが終わるラインを越えたらオープンコース(全員内側のレーン)を走るようになるんだよね。」
- はなこ 「そうだっけ!え, ちょっと待って。ということは, 内側のレーンの人の方が走る距離が短くて有利になっちゃうよね。」
- たろう 「そう!だからスタートラインで差をつけておくんだよ。」\\
- はなこ 「なるほど!私達の運動会のフィールドトラックでも, 内側のレーンを走る人と, 外側のレーンを走る人のスタートラインに何mの差をつければ良いのか計算してみようよ。」
- $(2)$ 図で2チームに分かれて4人が1人一周ずつ走るリレーを行うとき, 内側のレーンと外側のレーンのスタート位置には何mの差が必要か答えなさい。但し, 第1走者はセパレートコースを走り, 第2走者が最初のカーブが終わるラインを越えたらオープンコースを走るものとする。また, セパレートコースからオープンコースへ移る際の移動距離は考えないものとする。
- セパレートコースで差がつくのは, 半円3箇所分になるので, $\bigg(11\times2\times3.14\times\dfrac{1}{2}-10\times2\times3.14\times\dfrac{1}{2}\bigg)\times3=9.42$より, 9.42mの差が必要になります.
- たろう 「あ, 僕気づいたことがある!スタート位置の差にはレーンの幅が関連してくるんだ!」
- はなこ 「私はとっくに気づいていたよ。この法則でいうと, レーンの幅が2mになるとスタート位置の差は・・・。」
- $(3)$ 図でレーンの幅が2mのとき, スタート位置の差は何mになるか答えなさい。
- (2)同様計算すると, $\bigg(12\times2\times3.14\times\dfrac{1}{2}-10\times2\times3.14\times\dfrac{1}{2}\bigg)\times3=18.84$より, 18.84mの差が必要になります.


