問題
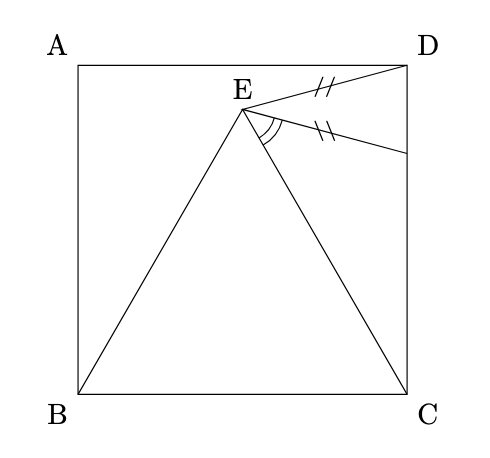
図のように, 正方形ABCDの中に正三角形EBCが入っています。同じ印のついた線の長さが等しいとき, 印のついた角度を求めなさい。但し, 解答は答えのみでよい。
解説
EからCDへの交点をFと置くと,
$\triangle{\mathrm{CDE}}$と$\triangle{\mathrm{EFD}}$は相似形なので$\angle{\mathrm{DCE}}=\angle{\mathrm{DEF}}=30^{\circ}$,
$\mathrm{CD}=\mathrm{CE}$より, $\angle{\mathrm{CED}}=(180^{\circ}-30^{\circ})\div2=75^{\circ}$
以上より, 印をつけた角度は$45^{\circ}$となります.


