問題
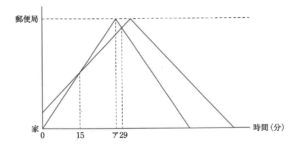
兄と弟が家と郵便局の間の道をそれぞれ一定の速さで往復しました。弟は兄より先に家を出発し、兄が家を出発したときに、弟は家から300m離れた地点にいました。また、兄が郵便局に着いたとき、弟は郵便局の240m手前にいました。下のグラフは、兄が家を出発してからの2人の進行の様子を表したものです。
- (1) アに当て嵌まる数はいくつですか。
- (2) 兄の歩く速さは分速何mですか。
- (3) 弟が郵便局に着いたとき、兄は郵便局から何m離れた地点にいましたか。
解説
- (1)
まずは、アの地点がどのようなところかを考えると、兄が郵便局に着いたタイミングだとわかります。
また、問題文から、このタイミングでの弟との差は240mとわかります。
更に、グラフを見ると、300mの差を15分で追いついたことがわかるので、1分当たりに縮まる距離は、
\(300\div15=20\)
より、20mとわかります。
これは、兄が弟を追い越した後、広がっていく距離とも等しいので、240mの差が開くまでにに、
\(240\div20-12\)
より、12分かかります。
以上よりアの値は、
\(15+12=27\)
で、27(分)とわかります。
\(\\\) - (2)
(1)より、兄と弟の1分当たりの速さの差が20mとわかったので、今度は速さの和が求められないかを考えます。
ここで、グラフの兄と弟が2回目に出会う地点に注目すると、240mの距離を2分間\((=29-27)\)で縮めていることがわかるので、兄と弟の1分当たりの速さの和は、
\(240\div2=120\)
より、120mとわかります。
これで、2数の和と差がわかったので、兄の速さを求めると、
\((120+20)\div2=70\)
より、分速70mとわかります。
\(\\\) - (3)
(2)より、兄の速さが分速70m、弟の速さが分速50mとわかったので、家から郵便局までの距離を求めると、
\(70\times27=1890\)
より、1890mとわかります。
次に、弟が郵便局に到着した時間を求めると、
\((1890-300)\div50=31.8\)
より、兄が出発してから31.8分後に郵便局に到着したことがわかります。
また、兄は出発して27分後に郵便局に到着し、弟が到着するまでの4.8分間\((=31.8-27)\)家に向かって移動しているので、
\(70\times4.8=336\)
より、郵便局から336m離れた地点にいるとわかります。