問題
中学1年生のうち、電車を利用している生徒は全体の\(\dfrac{1}{3}\)、バスを利用している生徒は全体の\(\dfrac{3}{8}\)でした。
また、電車とバスの両方を利用している生徒は全体の\(\dfrac{1}{12}\)、電車もバスも利用していない生徒は126人でした。
- 中学1年生は全部で何人ですか。
- 電車だけを利用している生徒は何人ですか。
解説
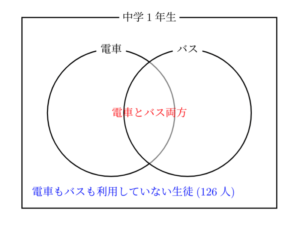
まずは、図のようにヴェン図を描いてみると、
\((\mbox{何かしらの交通機関を利用している生徒})=\)
\((\mbox{電車利用者})+(\mbox{バス利用者})-(\mbox{電車とバス両方の利用者})\)であるから、
\(\dfrac{1}{3}+\dfrac{3}{8}-\dfrac{1}{12}=\dfrac{5}{8}\)
より、中学1年生全体の\(\dfrac{5}{8}\)が何かしらの交通機関を利用しているとわかります。
このとき、電車とバスのどちらも利用していない生徒を考えると、
\(1-\dfrac{5}{8}=\dfrac{3}{8}\)
なので、全体の\(\dfrac{3}{8}\)であるとわかります。(少し勉強されている方には余事象と言った方がしっくりくるかもしれません。)
以上から、中学1年生全体の人数を求めると、
\(126\div\dfrac{3}{8}=336\)
となり、336人とわかります。- 電車を利用している生徒の人数は、
\(336\times\dfrac{1}{3}=112\)
より、112人で、このうちバスも利用している人数を引く必要があるので、
\(112-336\times\dfrac{1}{12}=84\)
となり、電車だけを利用している生徒は84人とわかります。


