問題
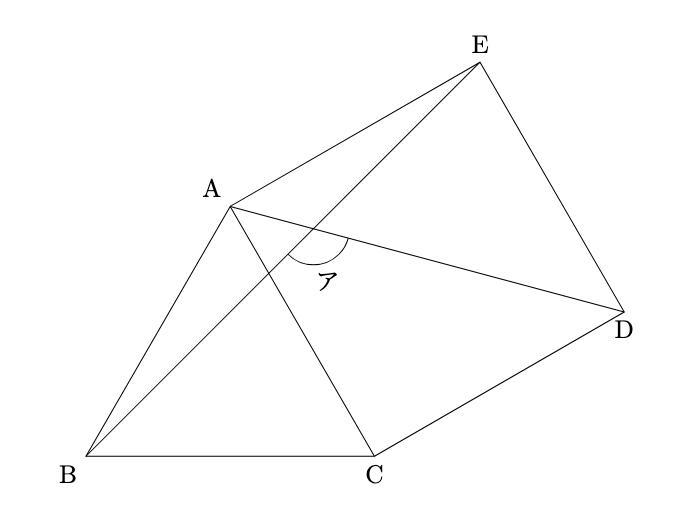
下の図において, 三角形ABCは正三角形, 四角形ACDEは正方形である. 角アの大きさは$\fbox{ }$度である.
解説
$\mathrm{AB}=\mathrm{AE}$より$\angle\mathrm{ABE}=\{180-(60+90)\}=15^{\circ}$となります.
ここで, 外角の定理から$\angle\mbox{ア}=\angle\mathrm{ABE}+\angle\mathrm{BAD}=15+(60+45)=120^{\circ}$より, $\fbox{ }=$$120$(度)とわかります.


