問題
商品についているバーコードには, 縞模様の下に13桁の数字が書かれていて, 商品名や値段などを機械で読み取ることができるようになっています. バーコードには, 機械が正しく読み取れたどうかを最後の数字(1桁目)でチェックできる仕組みがあり, この数字をチェックデジットといいます. チェックデジットは次の<例>のように計算されます.
<例> バーコードの13桁の数字 4946842506866
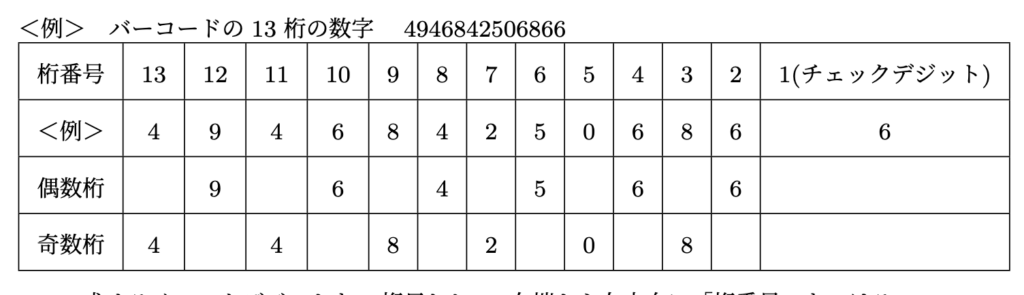
- 求めるチェックデジットを1桁目として, 右端から左方向に「桁番号」をつける.
- ① 全ての偶数桁の数字の和を求める. $9+6+4+5+6+6=36$
- ② ①の結果を3倍する. $36\times3=108$
- ③ 全ての奇数桁の数字の和を求める. 但し, 1桁目は除く. $4+4+8+2+0+8=26$
- ④ ②の結果と③の結果を足す. $108+24=134$
- ⑤ ④の結果の下1桁の数字を10から引いた数がチェックデジットとなる. 但し, ④の結果の下1桁の数字が0となった場合は, チェックデジットは0とする. $10-4=6$
次の問に答えなさい.
解説
- (1) バーコードの13桁の数字が49688135◻︎1714であるとき, ◻︎に当てはまる数を求めなさい.
- 例と同様に計算をすると, ①; $9+8+1+5+1+1=25$, ②; $25\times3=75$, ③; $4+6+8+3+◻︎+7=28+◻︎$, ④; $75+28+◻︎=103+◻︎$で, この値の下一桁が$10-4=6$となるので, ◻︎=3とわかります.
- (2) バーコードの13桁の数字が492507◻︎◻︎93250であるとき, 2つの◻︎に共通して当てはまる数を全て求めなさい.
- 例と同様に計算すると, ①; $9+5+7+◻︎+3+5=29+◻︎$, ②; $(29+◻︎)\times3=87+◻︎\times3$, ③; $4+2+0+◻︎+9+2=17+◻︎$, ④; $87+◻︎\times3+17+◻︎=104+◻︎\times4$で, この値の下一桁が0となるので, $◻︎\times4$の下一桁が6となり, ◻︎=4, 9とわかります.
- (3) バーコードの13桁の数字が4956317◻︎0◻︎8◻︎5であるとき, ◻︎には1つの偶数と2つの異なる奇数が入ります. このとき, 考えられるバーコードの数字は全部で何通りあるか求めなさい. 但し, 0は偶数とします.
- ◻︎に入る数字をそれぞれ, $a, b, c$として, 例と同様に計算すると, ①; $9+6+1+a+b+c=16+a+b+c$, ②; $(16+a+b+c)\times3=48+(a+b+c)\times3$, ③; $4+5+3+7+8=27$, ④; $\{48+(a+b+c)\times3+27\}=75+(a+b+c)\times3$で, この値の下一桁が$10-5=5$となるので, $(a+b+c)\times3$の下一桁が0となればよく, 偶数と奇数2つの組み合わせは,
- $(a, b, c)=(0,1,9), (0,3,7), (2,1,7),(2,3,5),(4,1,5),$
$(4,7,9),(6,1,3),(6,5,9),(8,3,9),(8,5,7)$
- $(a, b, c)=(0,1,9), (0,3,7), (2,1,7),(2,3,5),(4,1,5),$
- の10通りで, それぞれの並べ方は, $10\times3\times2\times1=60$より, 60通りとなります.
- ◻︎に入る数字をそれぞれ, $a, b, c$として, 例と同様に計算すると, ①; $9+6+1+a+b+c=16+a+b+c$, ②; $(16+a+b+c)\times3=48+(a+b+c)\times3$, ③; $4+5+3+7+8=27$, ④; $\{48+(a+b+c)\times3+27\}=75+(a+b+c)\times3$で, この値の下一桁が$10-5=5$となるので, $(a+b+c)\times3$の下一桁が0となればよく, 偶数と奇数2つの組み合わせは,


