問題
図のように, 半径4cmの円が3個ぴったりとくっついています. 斜線部分の面積の和は◻︎cm$^{2}$です.
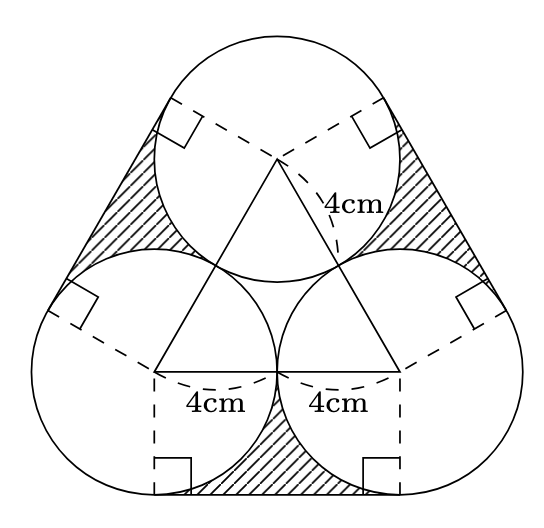
解説
以下のように補助線を引くと,
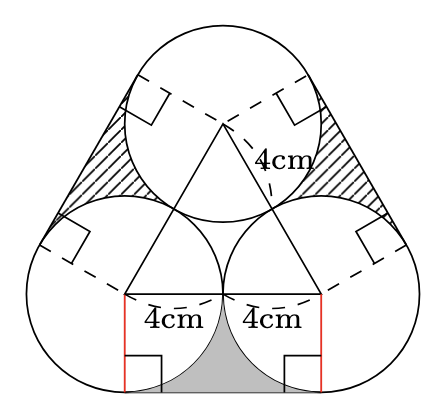
塗りつぶした部分の面積は, 長方形から四分円2つ分を引いたものになるので,
$4\times8-4\times4\times\dfrac{1}{4}\times2=6.88\mathrm{cm}^{2}$から,
求める面積は, $6.88\times3=20.64$より, $◻︎=20.64(\mathrm{cm}^{2})$となります.
 中学受験算数
中学受験算数