問題
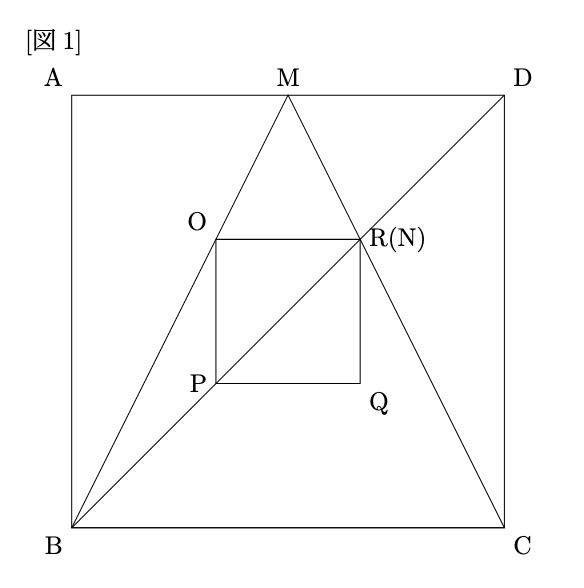
1辺が24cmの正方形ABCDがあり, 辺ADの中点をM, MCとDBの交点をNとする. 更に, 頂点OがBM上にあり辺ADと辺ORが平行である正方形OPQRを考える. 次の問に答えなさい.
解説
- (1) [図1]のように点Rが点Nと一致するとき, 辺OPの長さを求めなさい.
- $\mathrm{MR}:\mathrm{RC}=\mathrm{MD}:\mathrm{BC}=1:2$より, $\mathrm{OR}:\mathrm{BC}=\mathrm{MR}:\mathrm{MC}=1:(1+2)=1:3$なので,
$\mathrm{OP}=\mathrm{OR}=\dfrac{1}{3}\mathrm{BC}=$$8\mathrm{cm}$となります.
- $\mathrm{MR}:\mathrm{RC}=\mathrm{MD}:\mathrm{BC}=1:2$より, $\mathrm{OR}:\mathrm{BC}=\mathrm{MR}:\mathrm{MC}=1:(1+2)=1:3$なので,
- (2) [図2]のように点P, QがそれぞれDB, MC上にあるとき, 辺OPの長さを求めることを考える.
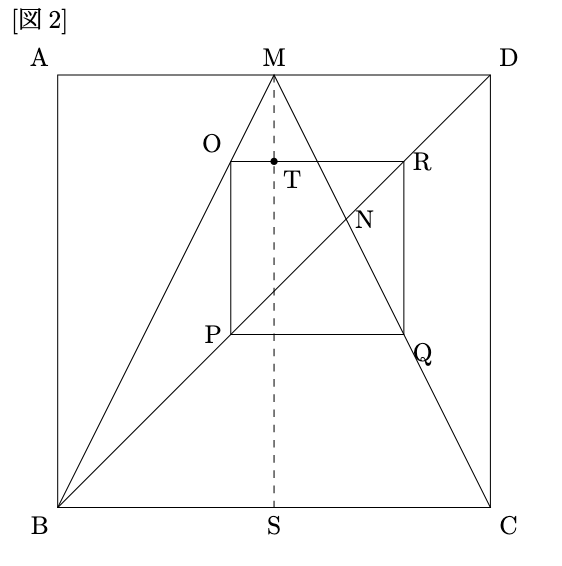
- (i) 辺BCの中点をSとし, MSと辺ORの交点をTとする. OTの長さは辺OPの長さの何倍か求めなさい.
- BDとMCの交点をUと置くと,
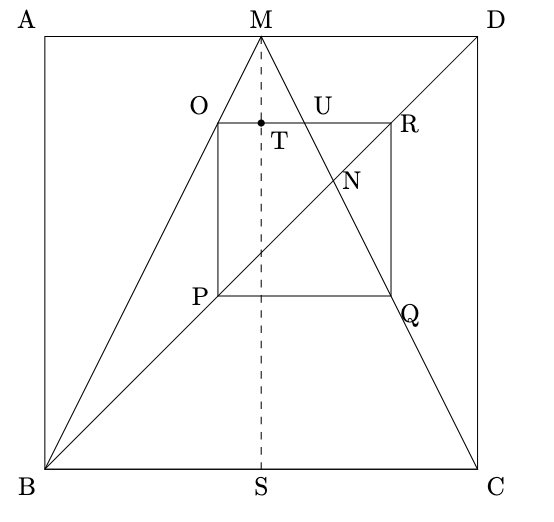
$\mathrm{UT}:\mathrm{TM}=\mathrm{UR}:\mathrm{RQ}=\mathrm{MD}:\mathrm{DC}=1:2$, $\mathrm{OT}:\mathrm{TM}=\mathrm{BS}:\mathrm{SM}=1:2$より, $\mathrm{OT}:\mathrm{OR}=1:(1+1+2)=1:4$から$\dfrac{1}{4}\mbox{倍}$となります.
- BDとMCの交点をUと置くと,
- (ii) 辺OPの長さを求めなさい.
- RからMDに下した垂線との交点をVと置くと,
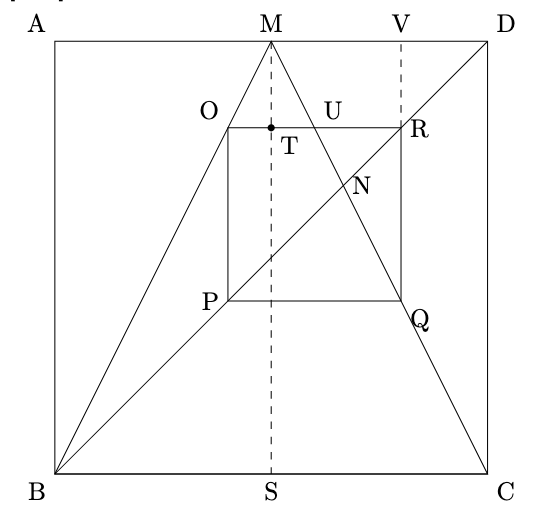
$\mathrm{MT}=\mathrm{VR}$から, $\mathrm{VD}=\dfrac{1}{2}\times\mathrm{PQ}=\dfrac{1}{2}\times\mathrm{OP}$,
また, $\mathrm{MV}=\mathrm{RU}+\mathrm{UT}=\dfrac{3}{4}\times\mathrm{OR}=\dfrac{3}{4}\times\mathrm{OP}$より,
$\mathrm{MD}=\mathrm{MV}+\mathrm{VD}=\bigg(\dfrac{1}{2}+\dfrac{3}{4}\bigg)\times\mathrm{OP}=12\mathrm{cm}$なので,
$\mathrm{OP}=12\times\dfrac{4}{5}=$$9.6\mathrm{cm}$となります.
- RからMDに下した垂線との交点をVと置くと,
- (i) 辺BCの中点をSとし, MSと辺ORの交点をTとする. OTの長さは辺OPの長さの何倍か求めなさい.


