問題
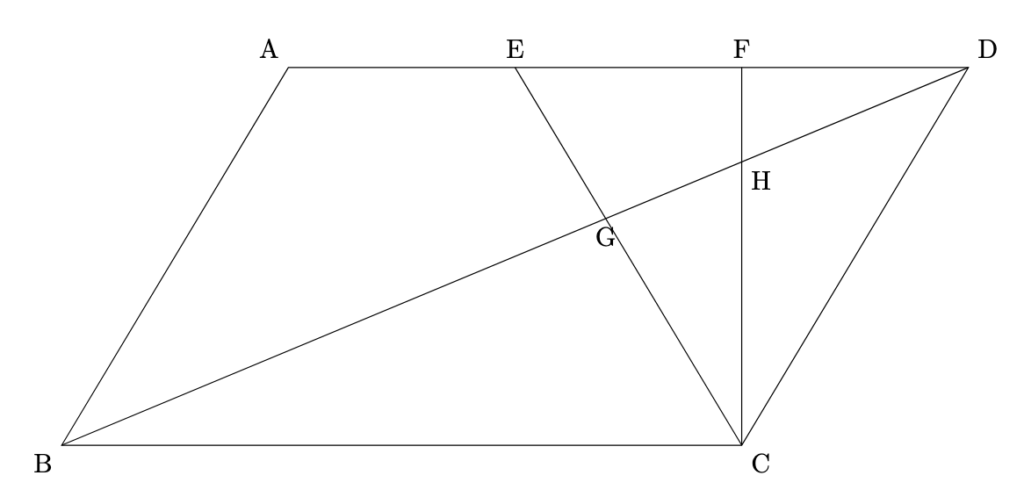
下の図のように, 平行四辺形ABCDがあります. 辺ADを三等分する点を頂点Aに近い方から順にE, Fとし, 対角線BDと直線CE, CFとの交点をそれぞれG, Hとします. このとき, 次の問に答えなさい.
解説
- (1) GHとHDの長さの比を求めなさい.
- 相似比を2箇所用いると, $\mathrm{BH}:\mathrm{HD}=3:1$, $\mathrm{BG}:\mathrm{GD}=3:2$から$\mathrm{BG}:\mathrm{GH}:\mathrm{HD}=12:3:5$より, $\mathrm{GH}:\mathrm{HD}=3:5$とわかります.
- (2) 三角形CGHと三角形HDFの面積の比を求めなさい.
- $\mathrm{GH}:\mathrm{HD}=3:5$より, $\triangle\mathrm{CGH}:\triangle\mathrm{DHC}=3:5$, $\mathrm{FH}:\mathrm{HC}=1:3$より$\triangle\mathrm{DFH}:\triangle\mathrm{DHC}=1:3$なので, 三角形CGHの面積を3とすると, 三角形HDFの面積は$3\times\dfrac{5}{3}\times\dfrac{3}{1}$から$\dfrac{5}{3}$となります.
以上より, $3:\dfrac{5}{3}=9:5$から, $9:5$となります.
- $\mathrm{GH}:\mathrm{HD}=3:5$より, $\triangle\mathrm{CGH}:\triangle\mathrm{DHC}=3:5$, $\mathrm{FH}:\mathrm{HC}=1:3$より$\triangle\mathrm{DFH}:\triangle\mathrm{DHC}=1:3$なので, 三角形CGHの面積を3とすると, 三角形HDFの面積は$3\times\dfrac{5}{3}\times\dfrac{3}{1}$から$\dfrac{5}{3}$となります.
- (3) 四角形ABGEと四角形EGHFの面積の比を求めなさい.
- 三角形CGHの面積を9として各三角形の面積を求めると,
三角形HDF; 5, 三角形FGH; 3, 三角形FEG; 8, 三角形BCG; 36, 三角形BEG; 24, 三角形ABE; 20
から, 四角形ABGEは$20+24=44$, 四角形EGHFは$3+8=11$より, $4:1$となります.
- 三角形CGHの面積を9として各三角形の面積を求めると,


