問題
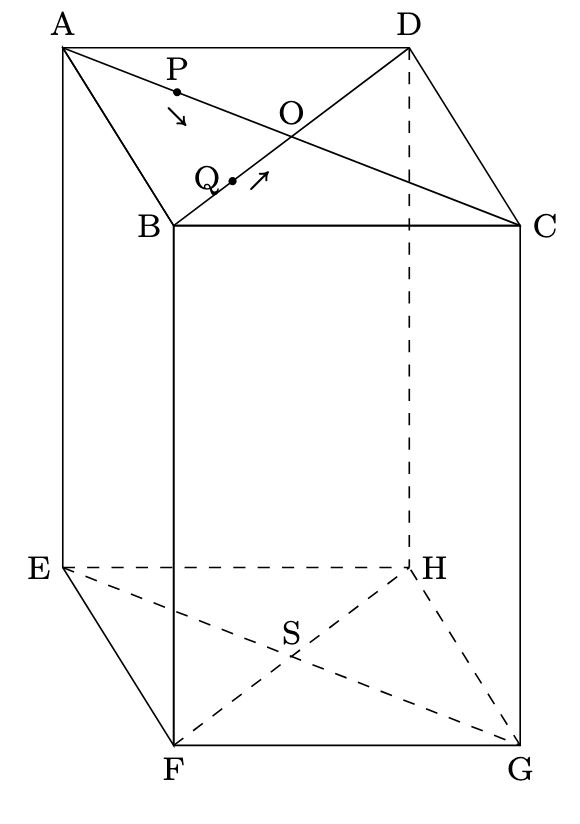
下の図のように, $\mathrm{AB}=8\mathrm{cm}$, $\mathrm{AD}=6\mathrm{cm}$, $\mathrm{AE}=9\mathrm{cm}$の直方体ABCD-EFGHがあります. 次の問に答えなさい.

解説
- (1) この直方体を, 3点B, D, Gを通る平面で切断したとき, 点Aを含む方の立体の体積を求めなさい.
- 切断面を以下のように書き込むと,

となり, Aを含む立体の体積は, 全体から三角錐GーBCDを引いたものなので, $8\times6\times9-8\times6\div2\times9\div3=360$より, 360cm$^{3}$となります.
- 切断面を以下のように書き込むと,
- (2) 長方形ABCDの対角線ACとBDの交点をO, 長方形EFGHの対角線EGとFHの交点をSとします. このとき, $\mathrm{AC}=10\mathrm{cm}$です. 今, 点Pは点Aを出発し, AC上をAからCに向かって毎秒2cmの速さで進み, 点Cで止まります. また, 点Qは点Bを出発し, BD上をBからDに向かって毎秒1cmの速さで進み, 点Dで止まります.
- ① 2点P, Qが同時に出発してから2秒後の四角錐S-CDPQの体積を求めなさい.
- 四角錐の体積の内, 高さの9cmは変わらないので, 底面積を求めればよいとわかります. ここで, 以下のように, 2秒後のPとQの位置関係を図に表すと,
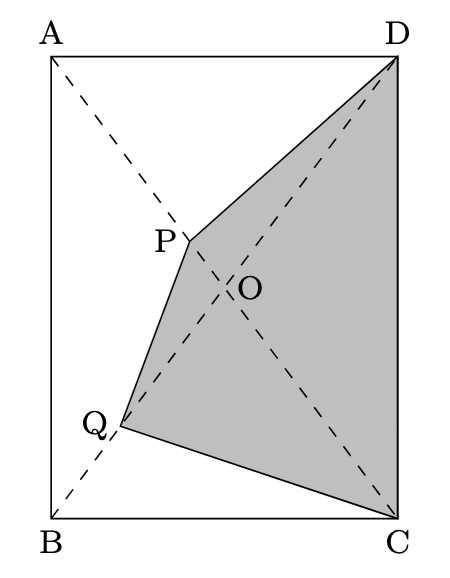
$\mathrm{AP}:\mathrm{PO}=4:1$, $\mathrm{BQ}:\mathrm{QO}=2:3$から, 四角形CDPQを三角形に分割して面積を求めると, $\triangle\mathrm{CDP}=8\times6\div2\times\dfrac{6}{10}=14.4\mathrm{cm}^{2}$, $\triangle\mathrm{PQO}=8\times3\div2\times\dfrac{1}{1+4}\times\dfrac{3}{2+3}=1.44\mathrm{cm}^{2}$, $\triangle\mathrm{CQO}=6\times4\div2\times\dfrac{3}{2+3}=7.2\mathrm{cm}^{2}$となり, 四角錐の体積は, $(14.4+1.44+7.2)\times9\div3=69.12$より69.12cm$^{3}$とわかります.
- 四角錐の体積の内, 高さの9cmは変わらないので, 底面積を求めればよいとわかります. ここで, 以下のように, 2秒後のPとQの位置関係を図に表すと,
- ② 2点P, Qが同時に出発してから何秒後かにPQとBCは平行になりました. このとき, 四角錐P-OQFSの体積を求めなさい.
- ①と同様に, まずは, PとQの位置関係を調べると, 以下のようになり,
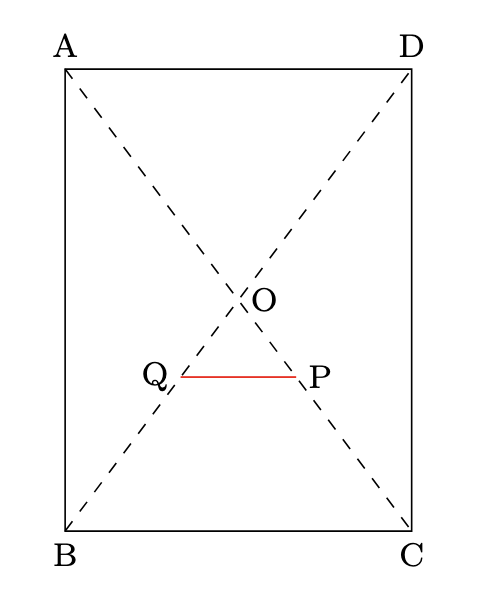
$\mathrm{BQ}=\mathrm{PC}$, $\mathrm{AP}:\mathrm{BQ}=4:2=2:1$から, $\mathrm{BQ}=\mathrm{PC}=10\times\dfrac{1}{1+2}=\dfrac{10}{3}\mathrm{cm}$とわかります, - 次に, 四角錐P-OQFSの位置関係を考えると,

底面積が台形OQFSであることがわかります. ここで, この四角錐の高さを考えると,
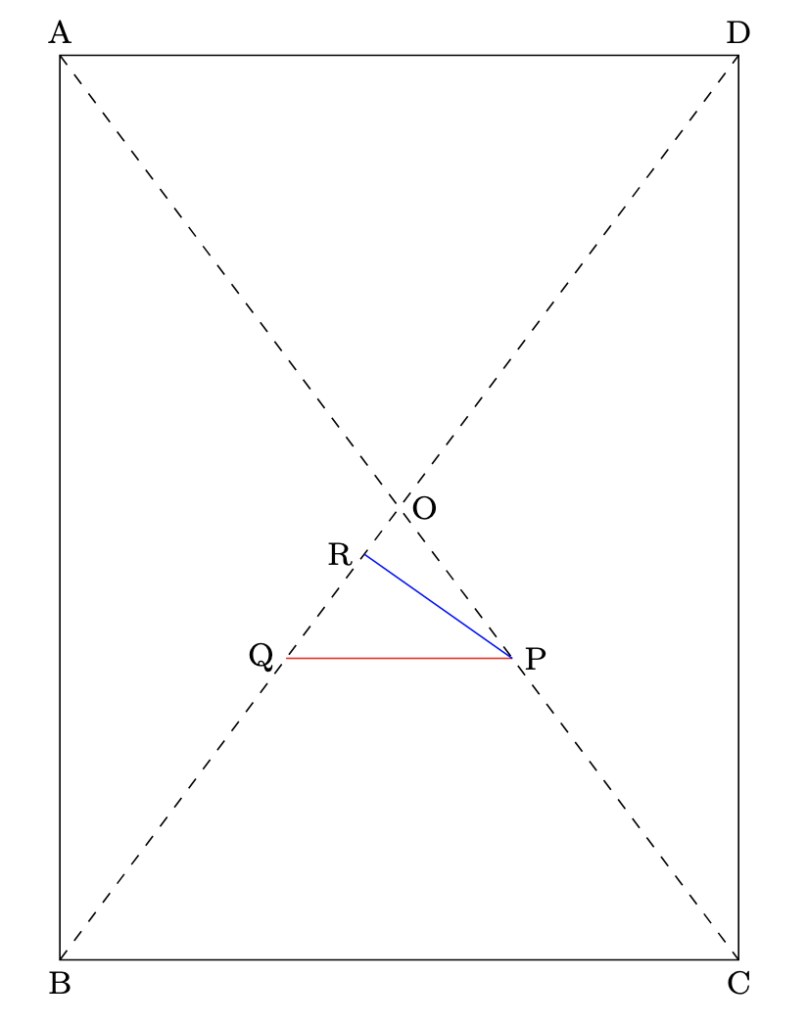
$\triangle\mathrm{OPQ}=6\times4\div2\times\dfrac{1}{3}\times\dfrac{1}{3}=\dfrac{4}{3}\mathrm{cm}^{2}$, $\triangle\mathrm{OPQ}=\mathrm{OQ}\times\mathrm{PR}\div2$から, $\mathrm{PR}=\dfrac{4}{3}\times\dfrac{3}{5}\times\dfrac{2}{1}=\dfrac{8}{5}\mathrm{cm}$から, 求める体積は, $\bigg(\dfrac{5}{3}+5\bigg)\times9\div2\times\dfrac{8}{5}\times\dfrac{1}{3}=16$より, 16cm$^{3}$となります.
- ①と同様に, まずは, PとQの位置関係を調べると, 以下のようになり,
- ① 2点P, Qが同時に出発してから2秒後の四角錐S-CDPQの体積を求めなさい.


