問題
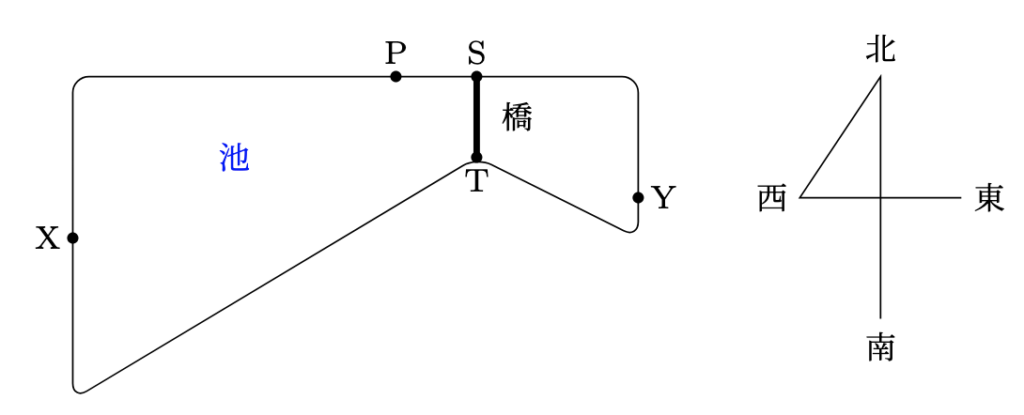
下の図のように, 池の周りに1周3.3kmのランニングコースと, 池に架かる橋があります. 橋はランニングコースのS地点とT地点の間に架かっています. A君とB君の2人がこのコースでランニングをするとき, 2人はそれぞれ一定の速さで走り, 走る速さの比は$10:9$です. 2人がP地点を同時に出発して, 池の周りを同じ向きに1周走りP地点に戻るとき, B君がP地点に戻るのは, A君がP地点に戻ってから1分50秒後です. 次の問に答えなさい.
解説
- (1) A君の走る速さは分速何mか求めなさい.
- 走る速さの比が$10:9$ということは, かかる時間の比は$\dfrac{1}{9}:\dfrac{1}{10}=9:10$より, A君が$\fbox{9}$, B君が$\fbox{10}$の時間で1周したとすると, 差分の$\fbox{1}$が1分50秒($1\dfrac{5}{6}$分)に当たるので, A君が1周した時間は$1\dfrac{5}{6}\times9=16.5$分より, A君の速さは, $3300\div16.5=200$から, 分速200mとわかります.
- (2) B君がP地点を出発してこのコースを一定の速さで走り始めました. 暫くしてから, A君がP地点を出発し, B君とは反対方向にこのコースを一定の速さで走ったところ, A君が出発してから7分30秒後に2人は初めて出会いました. A君が出発したのは, B君が出発してから何分何秒後か求めなさい.
- (1)から2人の速さはそれぞれ, A君が分速200m, B君が分速180mで, A君が7分30秒で走った距離は$200\times2.5=1500$mなので, B君の走った距離は$3300-1500=1800$m, 時間は$1800\div180=10$分なので, $10-7.5=2.5$より, A君が出発したのはB君が出発してから2分30秒後とわかります.
- (3) A君とB君の2人がP地点を同時に出発しました. A君はP→X→T→Yの順に一定の速さで走った後, Y地点で靴の紐を結び直すために立ち止まりました. その15秒後に, A君は再び一定の速さで走り始め, Y→S→Pの順に走ってP地点に戻りました. B君はP→X→Tの順に一定の速さで走った後, 池に架かる橋を1分40秒かけて歩いて渡り, SからPまでは再び一定の速さで走ったところ, A君よりも25秒先にP地点に戻りました. 橋の西側をS→P→X→T→Sの順に1周回るコースと, 東側をS→Y→T→Sの順に1周回るコースの距離の差は何kmか求めなさい.
- A君がP→X→T→Y→(15秒)→S→Pと走るのにかかった時間は$3300\div200+0.25=16.75$分, B君がP→X→T→(橋)→S→Pと走るのにかかった時間は$16.75-\dfrac{25}{60}=\dfrac{49}{3}$分, 橋を除いた時間は$\dfrac{49}{3}-1\dfrac{40}{60}=\dfrac{44}{3}$分となるので, 西側コースの距離は$180\times\dfrac{44}{3}=2640$m, 東側コースの距離は$3300-2640=660$mとそれぞれわかります. 以上から, 両コースの距離の差は$2640-660=1980$mより, 1.98kmとなります.


