問題
下の表は, ある小学校の6年1組と2組で行った10点満点の計算テストの得点をまとめたものです. この表からわかることとして正しいものを, ア〜カの中から全て選ぶと◻︎です.
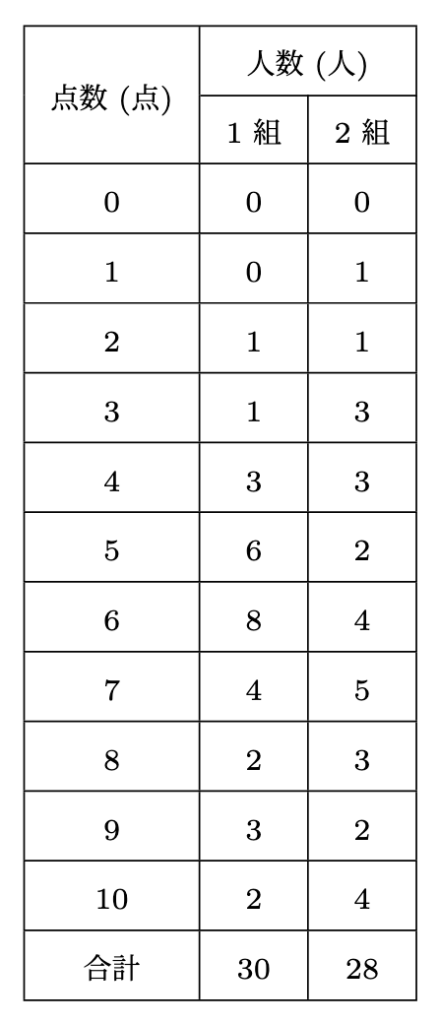
- ア 1組よりも2組の方が平均点が高い.
- イ 1組も2組も, 中央値は平均値より低い.
- ウ 1組も2組も, 中央値と最頻値は等しい.
- エ 1組と2組を合わせた58人の中央値と最頻値は等しい.
- オ 1組では, 中央値以下の生徒の人数は, クラス全体の丁度半分です.
- カ 2組では, 中央値以下の生徒の人数は, クラス全体の丁度半分です.
解説
選択肢にある各種値を求めると,
- 1組の平均点; $(0\times0+0\times1+1\times2+1\times3+3\times4+6\times5+8\times6+4\times7+2\times8+3\times9+2\times10)\div30=6.2$点
- 2組の平均点; $(0\times0+1\times1+1\times2+3\times3+3\times4+2\times5+4\times6+5\times7+3\times8+2\times9+4\times10)\div28=6.25$点
- 1組の中央値; 6点, 2組の中央値; 6.5点
- 1組の最頻値; 6点, 2組の最頻値; 7点
- 合計の中央値; 6点, 合計の最頻値; 6点
- 1組の中央値以下の割合; $(0+0+1+1+3+6+8)\div30\approx0.63$
- 2組の中央値以下の割合; $(1+1+3+3+2+4)\div28=0.5$
から, 正しいのは◻︎=ア, エ, カとなります.


