問題
下の図は, 底面が直角三角形である三角柱の展開図である. この三角柱について, 次の問に答えよ.
解説
- (1) 体積を求めよ.
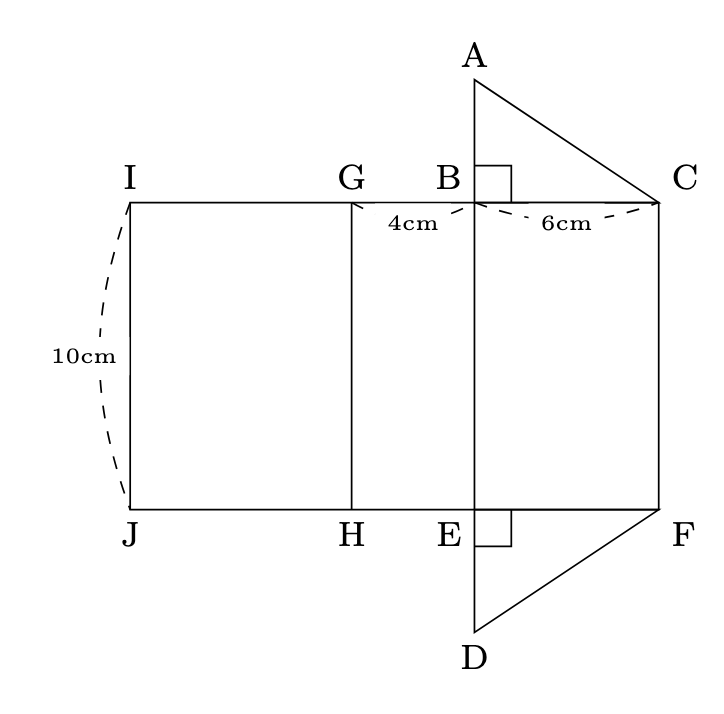
- 三角柱の体積は$\mbox{底面積}\times\mbox{高さ}$で求められるので, $6\times4\div2\times10=120$より, 120cm$^{3}$となります.
- (2) 下の図のような3点P, Q, Rを通る平面で切断したとき, 頂点Dを含む方の立体の体積を求めよ.
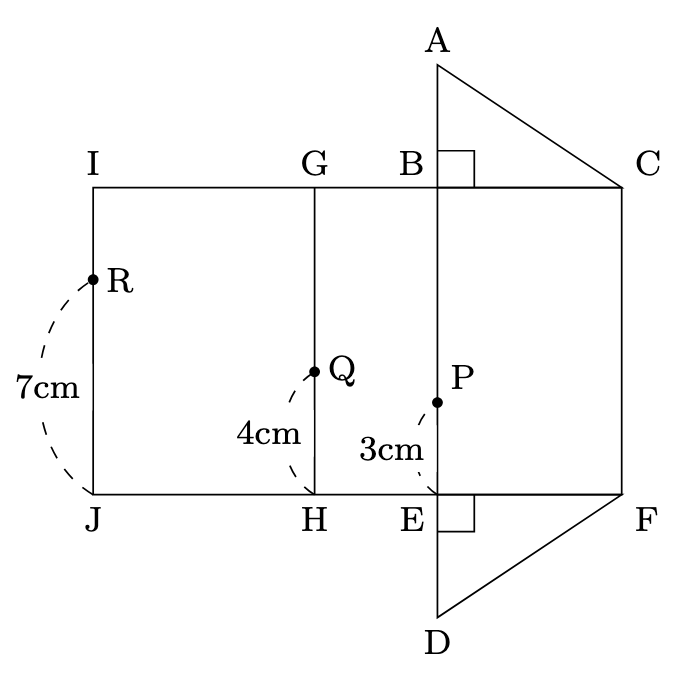
- 出来上がった立体を考えると,
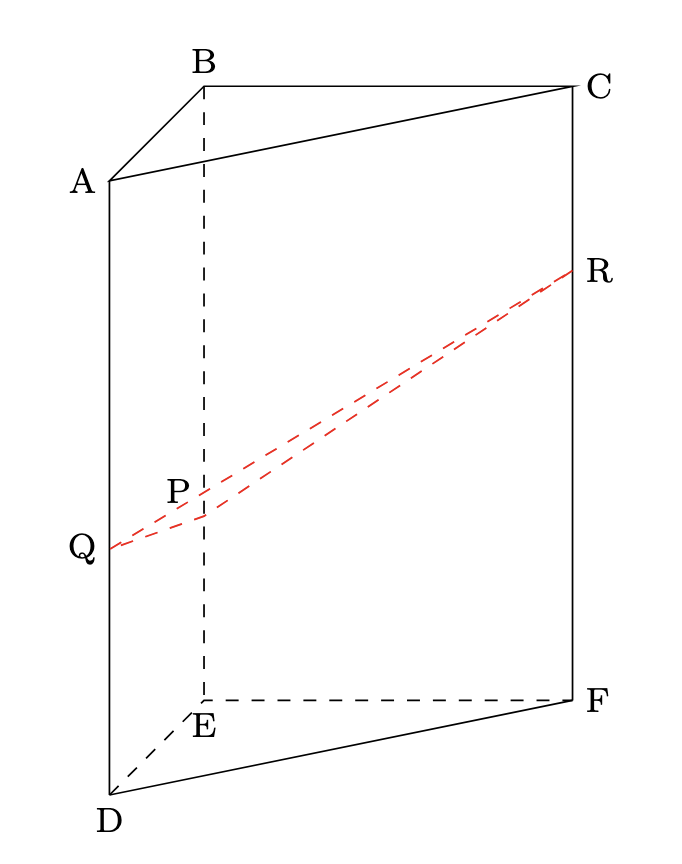
頂点Dを含む方の立体は, 平均の高さが$(3+4+7)\div3=\dfrac{14}{3}$cmの三角柱となるので, 求める体積は, $6\times4\div2\times\dfrac{14}{3}=56$より, 56cm$^{3}$とわかります.
- 出来上がった立体を考えると,
- (3) 下の図のように, MNとABが平行になるように辺AC, BC上にそれぞれ点M, Nをとる. 3点E, M, Nを通る平面で切断したとき, 頂点Cを含む方の立体の体積を求めよ.
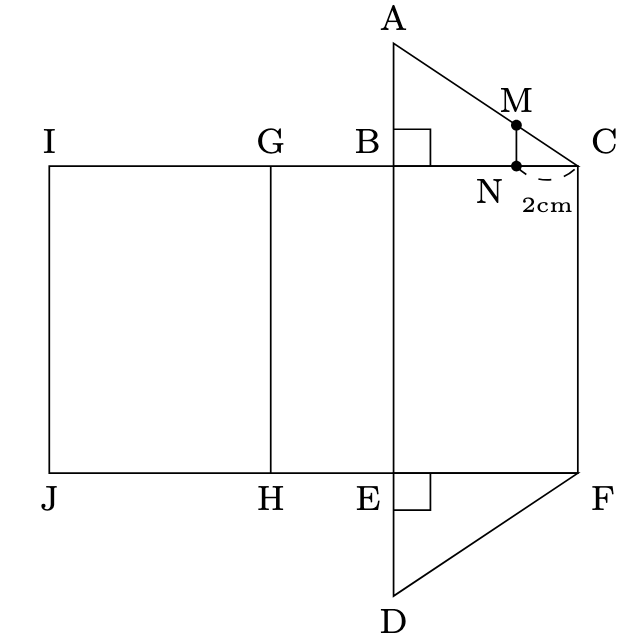
- 出来上がった立体を考えると,
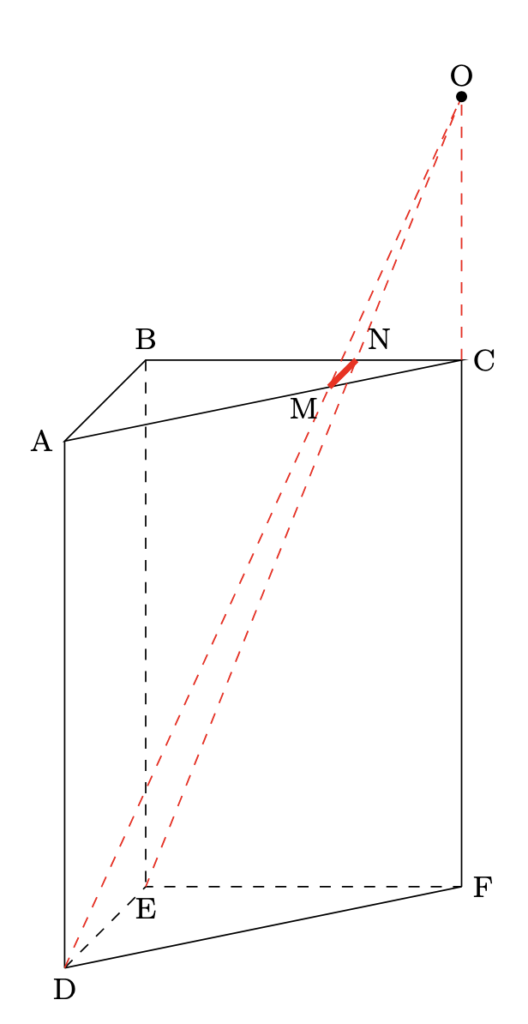
頂点Cを含む方の立体は, 円錐O-DEFから円錐O-MCNを引いたものなので, 求める体積は, $6\times4\div2\times15\div3\times\dfrac{(27-1)}{27}=57\dfrac{7}{9}$より, $57\dfrac{7}{9}\mathrm{cm}^{3}$とわかります.
- 出来上がった立体を考えると,


