問題
2桁の整数の内, 3でも7でも割り切れない数は◻︎個ある.
解説
以下のようにヴェン図を描くと,
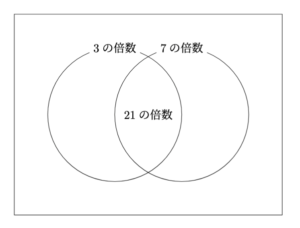
から, 3でも7でも割り切れない数は, 全体から, 3の倍数と7の倍数を足し, 21の倍数を引いたものを, 引けばよいとわかります.
- 3の倍数; $99\div3=33$, $9\div3=3$より, 30個
- 7の倍数; $99\div7=14\cdots1$, $9\div7=1\cdots2$より, 13個
- 21の倍数; $99\div21=4\cdots15$, $9\div21=0\cdots9$より, 4個
以上から, 求める個数は, $(99-10+1)-(30+13-4)=51$より, ◻︎=51(個)となります.


