問題
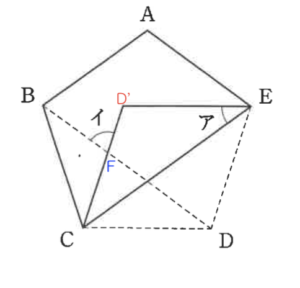
図のように正五角形ABCDEをCEで折り曲げました。
- ① 角アは何度ですか。
- ② 角イは何度ですか。
解説
- ①
ABCDEは正五角形なので、
\(CD’=ED’\)
より、△CD’Eは二等辺三角形とわかります。
また、正五角形の一つの内角の大きさは、
\(180\times(5-2)\div=108\)
より、108度とわかります。
以上から、
\(\mbox{ア}\times2+108=180\)
\(\mbox{ア}=36\)
となり、角アの大きさは36度とわかります。
\(\\\) - ②
△CDFに注目すると、∠CDF=36度、∠DCF=72度より、
∠CFD=72度とわかります。
このとき、対頂角が等しいので、
角イの大きさも72度とわかります。
補遺
多角形の問題で使用頻度の高い公式として、内角・外角の和を求めるものと、対角線の本数を求めるものがあるので挙げています。
- 3以上のnに対して、
\(\fbox{n角形の内角の和}=180^\circ\times(n-2)\)
\(\fbox{n角形の外角の和}-360^\circ\)
\(\\\) - 4以上のnに対して、
\(\fbox{n角形の対角線の本数}=(n-3)\times n\div2\)


