問題
・熱量の計算に関する次の文を読み, 後の問いに答えなさい。但し, 発泡スチロールの容器では, 熱は容器に吸収されたり, 容器の外に逃げたりしないものとします。
熱を数量的に表したものを熱量と言います。この熱量の単位はカロリーで表し, 1gの水の温度を1℃上げるのに必要な熱量を1カロリーとしています。例えば, 50gの水の温度を10℃上げるのに必要な熱量は, 500カロリーです。逆に, 1gの水が他のものへ1カロリーの熱量を与えると, 水の温度は1℃下がります。
この考えから計算すると, 例えば, 20℃の水100gと80℃の水50gを混ぜ合わせるとき, $(20\times100+80\times50)\div(100+50)=40$より, 水全体の温度は40℃になります。
また, 0℃の氷1gを0℃の水1gにかえるには, 80カロリーの熱量が必要です。
- (1)発泡スチロールの容器に15℃の水50gが入っており, 90℃の水100gを継ぎ足しました。水の温度は何℃になったでしょうか。
- (2)発泡スチロールの容器に20℃の水240gが入っており, 70℃の水を何gか継ぎ足しました。水の温度が40℃になったとすると, 70℃の水を何g継ぎ足しましたか。
- (3)発泡スチロールの容器に入った70℃の水160gの中に, 0℃の氷40gを入れると完全に溶けて混ざりました。水の温度は何℃になったでしょうか。
ここで, 発泡スチロールの容器の中に水と共に重さ100gの鉄球を入れて実験を続けました。鉄球の温度は容器の中の水の温度と同じになり, 水と同じように熱のやり取りをするものとします。
- (4)発泡スチロールの容器に30℃の水240gと30℃の鉄球100gが入っていました。ここに90℃の水50gを入れると40℃になりました。このとき, 鉄1gの温度を1℃上げるのに必要な熱量は, 水1gの温度を1℃上げるのに必要な熱量の何倍と考えられますか。最も相応しいものを次のア〜オから1つ選び, 記号で答えなさい。
- ア. 0.01倍
- イ. 0.1倍
- ウ. 1倍
- エ. 10倍
- オ. 100倍
- (5)発泡スチロールの容器に80℃の鉄球100gと何gかの水が入っていました。ここに8℃の水60gを入れると62℃になりました。最初に発泡スチロールの容器に入っていた水の重さは何gでしたか。
模範解答
- (1) 65℃
- Tips
- 0℃の状態に比べてどれだけ熱量が余分にあるかでカロリー計算をします. 15℃の水50gで, $15\times50=750$カロリーであり, 90℃の水100gで$90\times100=9000$あります. これらを混ぜ合わせると, 合計$750+9000=9750$カロリーになり, これを$50+100=150g$の水で分け合っているので, 水の温度は平均して, $9750\div150=65$℃になります.
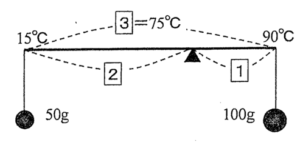
*図のように天秤を用いて解くこともできます.
- 0℃の状態に比べてどれだけ熱量が余分にあるかでカロリー計算をします. 15℃の水50gで, $15\times50=750$カロリーであり, 90℃の水100gで$90\times100=9000$あります. これらを混ぜ合わせると, 合計$750+9000=9750$カロリーになり, これを$50+100=150g$の水で分け合っているので, 水の温度は平均して, $9750\div150=65$℃になります.
- Tips
-
-
- 90―75×1÷(1+2)=65℃
-
- (2) 160g
- Tips
- 元々容器に入っていた20℃の水240gが得た熱量は, $(40-20)\times240=4800$カロリーです. この熱量を70℃の水から奪ったので, $(70-40)\times(水の重さ)=4800$と立式できます. これを解くと, $(水の重さ)=4800÷30=160$gになります.
- Tips
- (3) 40℃
- Tips
- 0℃の氷40gを解かして0℃の水40gにするには, $80\times40=3200$カロリーが必要で, 70℃の水160gの持つ熱量は0℃の水に比べて$70\times160=11200$カロリー多いので, 温度変化に使えるカロリーは, $11200―3200=8000$カロリーとなります. これを$40+160=200$gで分け合うので, $8000\div200=40$℃になります.
- Tips
- (4) イ
- Tips
- 温度の高い方から低い方に移動した熱量と温度が低い方が受け取った熱量が等しいことを利用します. 90℃の水50gが40℃になる間に失った熱量は, $(90-40)\times50=2500$カロリーで, 容器に元々入っていた30℃の水240gが40℃になる間に受け取った熱量は, $(40-30)\times240=2400$カロリーとなります. これらの差分に当たる, $2500-2400=100$カロリーが, 鉄球が受け取った熱量になります. 100gの重さの鉄球の温度も, 容器に入っている水と同じように30℃から40℃に10℃上昇していますが, 鉄球が受け取った熱量は$10\times100=1000$カロリーとはならず, 100カロリーです. これは, 水と同じ熱量を受け取っても, 鉄の方が温度が上がりやすいためです. 鉄1gの温度を1℃上げるのに必要な熱量と, 水1gの温度を1℃上げるのに必要な熱量を比べると, $100\div1000=0.1$より, 水の0.1倍のカロリーで足りることがわかります. この値を比熱といい, 選択肢のイが正解となります. また, 視点を変え, 100gの鉄球を水で賄うとすると, $100\times0.1=10$g分になるので, 30℃の水$240+10=250$gと90℃の水50gを混ぜ合わせた場合と考えることができます.
- Tips
- (5) 170g
- Tips
- (4)の結果から, 100gの鉄球は10gの水と考えればよいので, 後から入れた8℃の水60gが62℃になるまでに得た熱量は, $(62-8)\times60=3240$カロリーとなります. 初めに入っていた80℃の鉄球100gが62℃になるまでに奪われた熱量は, $(80-62)\times100\times0.1=180$かカロリーなので, 80℃の水が奪われた熱量は$3240―180=3060$カロリーです. 以上から, 初めに容器に入っていた80℃の水の重さを求めると, $(80―62)\times(水の量)=3060$より, これを解くと170gとなります.
- Tips


