問題
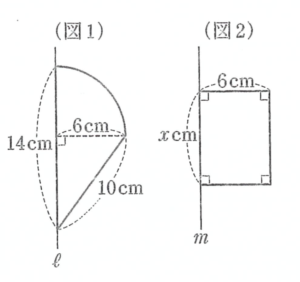
図1において直線ℓを軸として1回転させてできる立体と、図2において直線mを軸として1回転させてできる立体について、次の問に答えなさい。
- (1) 2つの立体の体積が等しいとき、\(x\)の値を求めなさい。
- (2) 2つの立体の表面積が等しいとき、\(x\)の値を求めなさい。
解説
- (1) 図1の立体の体積は、半径6cmの半球と底面の半径が6cmで高さが8cmの円錐の合計なので、
\(\dfrac{4}{3}\pi\times6^3\times\dfrac{1}{2}+6\times6\times\pi\times8\times\dfrac{1}{3}\)
\(=144\pi+96\pi\)
\(=240\pi\)
より、240\(\pi\)㎠になります。また、図2の立体の体積は、底面の半径が6cmで高さが\(x\)cmの円柱なので、
\(6\times6\times\pi\times x=36\pi x\)
となり、この値が240\(\pi\)㎠より、
\(240\pi=36\pi x\)
\(x=\dfrac{20}{3}\) - (2) 図1の立体の表面積は、半径6cmの半球と半径が10cmの扇形の合計なので、
\(4\pi\times6^2\times\dfrac{1}{2}+10\times10\times\pi\times\dfrac{6}{10}\)
\(=72\pi+60\pi\)
\(=132\pi\)また、図2の立体の表面積は、半径6cmの円2つと側面の長方形の合計なので、
\(6\times6\times\pi\times2+6\times2\times\pi\times x\)
\(=72\pi+12\pi x\)
となり、この値が\(132\pi\)㎠より、
\(132\pi=72\pi+12\pi x\)
\(x=5\)


