問題
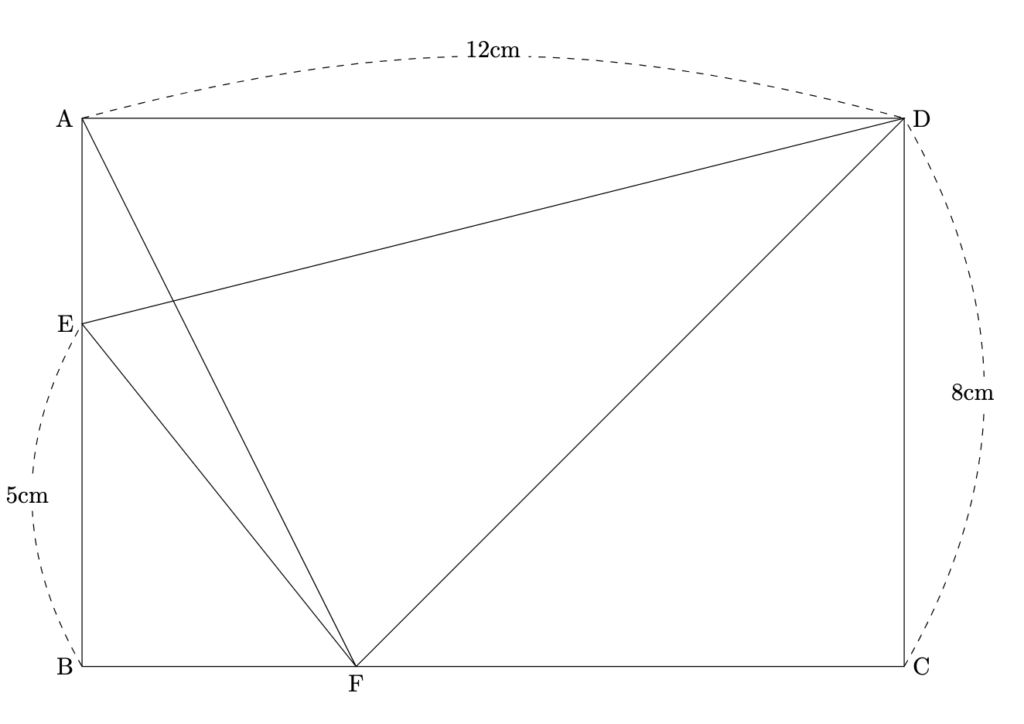
次の四角形は長方形で, 点EはAB上, 点FはBC上にあります。三角形EFDの面積が36cm$^{2}$のとき, 後の問に答えなさい.
解説
- $(1)$ 三角形AEDの面積は何cm$^{2}$ですか.
- $3\times12\div2=$$18\mathrm{cm}^{2}$
- $(2)$ 三角形AEFの面積は何cm$^{2}$ですか.
- $\triangle\mathrm{AEF}=\triangle\mathrm{AED}+\triangle\mathrm{EFD}-\triangle\mathrm{AFD}$より, $18+36-12\times8\div2=$$6\mathrm{cm}^{2}$となります.
- $(3)$ FCの長さは何mですか.
- $\mathrm{FC}=\mathrm{BC}-\mathrm{BF}$, $\triangle\mathrm{AEF}=\mathrm{AE}\times\mathrm{BF}\div2$より, $\mathrm{BF}=6\times2\div3=4\mathrm{cm}$となるので, $\mathrm{FC}=12-4=$$8\mathrm{cm}$とわかります.


