問題
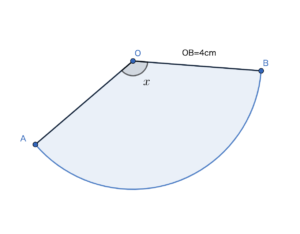
図のような半径が4cmの扇形OABがあり、\( \stackrel{\frown}{\mbox{AB}} \)の長さは\(3\pi\)cmである。
- (1) 中心角\(x\)の値を求めなさい。
- (2) 扇形OABの面積を求めなさい。
解説
- (1) 中心角を\(x\)として扇形の弧の長さを求める式を立てると、
\(4\times 2\times \pi\times \dfrac{x}{360}=3\pi\)
\(x=3\pi\times360\div8\pi\)
\(x=135\)
となり、中心角\(x\)の大きさは135度とわかります。 - (2) 一般的に扇形の面積\(S\)は、半径を\(r\)、弧の長さを\(l\)とすると、
\(S=\dfrac{1}{2}rl\)
で求められるので、今回の場合に当てはめれば、
\(\dfrac{1}{2}\times4\times3\pi=6\pi\)
より、扇形OABの面積は\(6\pi\)㎠とわかります。


