問題
・電流と発熱の関係について, 次の問いに答えなさい。
電熱線に電流を流すと発熱します。電熱線を水の中に入れて電流を流し, 水の温度上昇について調べる実験を行いました。
その結果, 水の上昇温度は, 電熱線の長さ, 電流を流した時間, 水の量などの条件によって変わることがわかりました。
そこで, 図のような実験装置を使い, 電源の電圧は全て同じに揃え, それ以外の条件を色々変えて, 流れた電流の大きさと水の温度上昇を測りました。(表1)はその結果を示しています。但し, 電熱線の材質, 太さは全て同じとします。
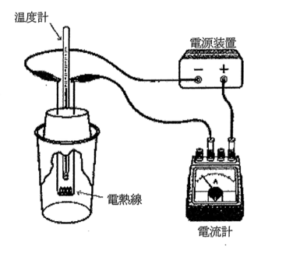
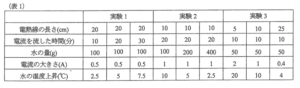
- (1)実験結果から, 電流の大きさは何と関係があることがわかりますか。次のア〜ウから1つ選び, 記号で答えなさい。
- ア. 電熱線の長さ
- イ. 電流を流した時間
- ウ. 水の量
- (2)実験結果から, 水の温度上昇についてどのようなことがわかりますか。次の文の空欄(X), (Y)に当てはまる言葉を後のア〜カから1つずつ選び, それぞれ記号で答えなさい。
実験1の結果から水の温度上昇は電流を流した時間に(X), 実験2の結果から(Y)に反比例する。- ア. 比例し
- イ. 反比例し
- ウ. 関係なく
- エ. 電熱線の長さ
- オ. 水の量
- カ. 電流の大きさ
- (3)長さ20cmの電熱線を用いて, 水を200gにして40分間電流を流すと, 水の温度上昇は何℃になりますか。
- (4)長さ30cmの電熱線を用いて, 水を250gにして30分間電流を流すと, 水の温度上昇は何℃になりますか。
次に, 水を換えて液体Aを用いて, 電源の電圧, 電熱線の材質, 太さは今までと同じ条件で実験4を行いました。(表2)はその結果を表しています。
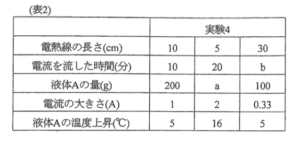
- (5)この液体Aと水では, どちらが温まりやすいですか。次のア〜ウから1つ選び, 記号で答えなさい。
- ア. 液体A
- イ. 水
- ウ. 同じ
- (6)(表2)の空欄a, bに当てはまる値を答えなさい。
模範解答
- (1) ア
- (2) X; ア Y; オ
- Tips
- 実験結果を整理すると以下のようになります.
- 実験1からわかることは, 他の条件を変えずに電流を流した時間を10分, 20分(2倍), 30分(3倍)と変えると, 水の温度上昇は2.5℃, 5℃(2倍), 7.5℃(3倍)と変わり, 正比例していることがわかります.
- 実験2からわかることは, 他の条件を変えずに水の量を100g, 200g(2倍), 400g(4倍)と変えると, 水の温度上昇は10℃, 5℃($\frac{1}{2}$倍), 2.5℃($\frac{1}{4}$倍)と変わり, 反比例していることがわかります.
- 実験3からわかることは, 他の条件を変えずに電熱線の長さを5cm, 10cm(2倍), 25cm(5倍)と変えると, 電流の大きさは2A, 1A($\frac{1}{2}$倍), 0.4A($\frac{1}{5}$倍)と変わり, 反比例していることがわかります. 更に, 電流の大きさが2A, 1A($\frac{1}{2}$倍), 0.4A($\frac{1}{5}$倍)と変わると, 水の温度上昇は20℃, 10℃($\frac{1}{2}$倍), 4℃($\frac{1}{5}$倍)と変わり, 正比例していることもわかります.
- 実験結果を整理すると以下のようになります.
- Tips
- (3) 5℃
- Tips
- 各項目と比例反比例の関係を考えると, (表1)の実験2の中央列と問題の条件を比べると,
・長さ10cm, 水200g, 時間20分→温度上昇5℃
・長さ20cm, 水200g, 時間40分
より, 長さが2倍で温度上は1/2倍, 時間が2倍で温度上昇も2倍なので, 温度上昇は, $5\times\frac{1}{2}\times2=5$℃とわかります.
- 各項目と比例反比例の関係を考えると, (表1)の実験2の中央列と問題の条件を比べると,
- Tips
- (4) 2℃
- Tips
- (3)同様に条件を比べると,
・長さ10cm, 水200g, 時間20分→温度上昇5℃
・長さ30cm, 水250g, 時間30分
より, 長さが3倍で温度上昇は$\frac{1}{3}$倍, 水が$\frac{5}{4}$倍で温度上昇は$\frac{4}{5}$倍, 時間が$\frac{3}{2}$倍で温度上昇も$\frac{3}{2}$倍なので, 温度上昇は, $5\times\frac{1}{3}\times\frac{4}{5}\times\frac{3}{2}=2$℃とわかります.
- (3)同様に条件を比べると,
- Tips
- (5) ア
- Tips
- (表1)の実験3の中央列と, (表2)の実験4の左列を比較すると,
(水) ・長さ10cm, 水50g, 時間10分→温度上昇10℃
(液体A) ・長さ10xm, 液体A200g, 時間10分→温度上昇5℃
ここで, 液体Aの量を50gにすると, 温度上昇は$5\times4=20$℃になるので, 液体Aの方が温まりやすいとわかります.
- (表1)の実験3の中央列と, (表2)の実験4の左列を比較すると,
- Tips
- (6) a; 250 b; 15
- Tips
- 数値の出揃っている左列を元に中央列を比較すると,
・長さ10cm, 液体A200g, 時間10分, 電流1A→温度上昇5℃
・長さ5cm, 液体A ag, 時間20分, 電流2A→温度上昇16℃
ここで, 液体A以外の条件を揃えていくと, 長さを10cm(2倍)にすると電流, 温度上昇共に$\frac{1}{2}$倍(連動することに注意), 時間を10分($\frac{1}{2}$倍)にすると, 温度上昇も$\frac{1}{2}$倍になるので, 温度上昇は$16\times\frac{1}{2}\times\frac{1}{2}=4$℃になります. ここで, 液体量と温度上昇は反比例の関係にあるので, $a=200\times\frac{5}{4}=250$g, とわかります. - 同様に左列と右列を比較すると,
・長さ10cm, 液体A200g, 時間10分, 電流1A→温度上昇5℃
・長さ30cm, 液体A100g, 時間b分, 電流0.33A→温度上昇5℃
ここで, 時間以外の条件を揃えていくと, 長さを30cm($\frac{1}{3}$倍)にすると, 電流, 温度上昇共に3倍, 液体Aの量を200g(2倍)にすると, 温度上昇は$\frac{1}{2}$倍になるので, 温度上昇は$5\times3\times\frac{1}{2}=7.5$℃になります. ここで, 時間と温度上昇は比例の関係にあるので, $b=10\times$\frac{7.5}{5}$=15$分, とわかります.
- 数値の出揃っている左列を元に中央列を比較すると,
- Tips