例題
不等式 $5x-3>x+a$ について, 次の問いに答えよ.
- (1) 解が $x>2$ となるように, 定数 $a$ の値を定めよ.
- (2) 解が $x=3$ を含むように, 定数 $a$ の範囲を定めよ.
指針
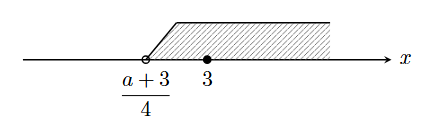
不等式を解き, その解を数直線上に表すと分かりやすい.
解答
- (1) $5x-3>x+a$から, $4x>a+3$よって$x>\dfrac{a+3}{4}$
解が $x>2$ であるから, $\dfrac{a+3}{4}=2$故に$a=5$. - (2) $x=3$ が$x>\dfrac{a+3}{4}$を満たすから, $\dfrac{a+3}{4}<3$
よって$a+3<12$, すなわち$a<9$.