問題
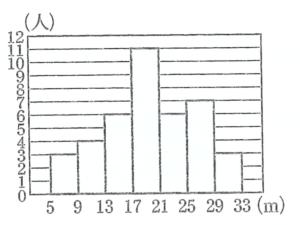
下の図はあるクラス40人のハンドボール投げの記録をヒストグラムに表したものである。このヒストグラムでは、例えば、6〜9の階級では、ハンドボール投げの記録が5m以上9m未満の人数が3人であったことを表している。また、ハンドボール投げの記録の中央値は18mであった。このとき、次の各問に答えなさい。但し、記録の値は全て自然数である。
- (1) ハンドボール投げの記録の最頻値を求めなさい。
- (2) ハンドボール投げの記録で、25m以上投げた人の相対度数を求めなさい。
- (3) ハンドボール投げの記録を小さい方から並べたとき、20番目の値をa、21番目の値をbとする。このヒストグラムから考えられるa・bの組は2つある。その2つの組を求めなさい。
- (4) ハンドボール投げの記録の平均値を求めなさい。
解説
- (1)
最頻値(モード)とは、データの中で最も個数の多い値を指し、ヒストグラムを見ると、17m以上21m未満が11人で最多となっています。
今回のように、最頻値に幅がある場合は、階級値を求める必要があるので、
\((17+21)\div2=19\)
より、19mとなります。
\(\\\) - (2)
相対度数とは、データの中である階級の度数がどの程度の割合であるかを指すので、まずは、25m以上投げた人の度数を数えると、
\(7+3=10\)
より、10人とわかります。
また、全体の度数は40人なので、相対度数を求めると、
\(10\div40\times100=25\)
より25%とわかります。
\(\\\) - (3)
中央値とは、データを小さい方から並べた際に中央に来る値を指すので、中央値が18mなら、aとbの合計は、
\((a+b)\div=2=18\)
\(a+b=36\)
より、36とわかります。
また、20番目の値と21番目の値は、共に17m以上25m未満の階級に属しているので、考えられるa・bの値の組は、
\((a, b)=(17, 19), (18, 18)\)の2つとわかります。
\(\\\) - (4)
平均値とは、データの測定値の合計をデータの個数で割った値を指すので、各ヒストグラムの階級値と度数から測定値の合計を求めると、
\(7\times3+11\times4+15\times6+19\times11\)
\(+23\times6+27\times7+31\times3=884\)
となり、また、データの個数は40なので、
\(884\div40=22.1\)
より、平均値は22.1mとなります。


